ヘーゲルの言葉は難しくて私にはよくわからない.本書を読む上では「ものの集まりをひと塊にして,それをひとつのものとみなす」という理解で十分であろう.
「たびたび引き合いに出される」というのは,p.43 で部分集合をひとつの要素とみなすところと,p.80 で類をひとつのものと考えるところ.
「集合」を知らないものとして書かれている.1952年当時の読者は集合になじみがなかったのだと思う.
遺産相続の例(p.17)をまねるのが簡単であろう.奇数番目のリンゴをミカンに対応させ,偶数番目を余らせる.
高校までの数学では明確でないが,微分積分学の基礎は実数論にあるため.
カントールの定義は p.13 参照.
定規とコンパスで任意の角を 3 等分することができないことはよく知られている.
この問題は,
\(a=\sin \theta\)
という長さが与えられたとき,\(x=\sin (\theta/3)\)
という長さが作図できるかとして扱う.3倍角の公式 \(\sin 3\phi=3 \sin \phi -4 \sin^3\phi\) より,
\(a=3x-4x^3\)
となるから,3 次方程式の問題になる.もちろん 0 でもよい.
背理法のこと.
直前の議論からは「直線上」ではなく「線分上」であろう.ここから先の話の流れから見ても「線分上」の間違いと思われる.
線分(あるいは直線)上の点全体の計数を「連続の濃度(cardinality of the continuum)」という.「\(\mathfrak{c}\)」は continuum の頭文字をドイツ文字で表記したもの.あとの章でもよく出てくるから覚えておく必要がある.
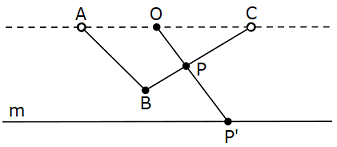
図について説明しておく.
直線 \({\rm AB}\) を \(m\) として図示したのが下図.線分は端点を含まず,折ったものが \({\rm ABC}\) である.\({\rm A,\, O,\, C}\) は直線 \(m\) と平行な直線上にとる.テキストでは折れ線と直線がくっついているが,この図のように離してもよい.
「中央で折って」とあるが,適当なところで折っている.正確に線分の中点で折れば \({\rm AB=BC}\) になる.
この注釈は神経質すぎるので,気になる人以外は読まない方がよい.
正方形内の点なので \(0\lt x \lt 1,\, 0 \lt y\lt 1\) としたいところだが,以下の議論で \(z=0.9191919\cdots\) のとき \(x=0.99999\cdots =1\) となるためうまくない.
\( 0 \lt x\leqq 1,\, 0 \lt y\leqq 1,\, 0 \lt z\leqq 1 \)とするのがよい.そして,0.2 と 0.19999… という 2 通りの表し方があるときは後者をとり,テキスト p.187 の「注 (2) 」にある区切りを採用するのが厳密である.
このとき,\((x,y) \leftrightarrow z\) という一対一対応があることになる.
無限集合に要素を 1 つ加えても計数は変わらない(p.40の注釈できちんと示す).よって,\(0 \lt x \lt 1\) と \(0 \lt X \leqq 1\) の間には,
\( x \leftrightarrow X \)という一対一対応がある.同様に,\(0\lt Y\lt 1,\, 0\lt Z\lt 1\) とするとき,\(y \leftrightarrow Y, z \leftrightarrow Z\) の一対一対応がある.
以上のことから,
\((X,Y) \leftrightarrow (x,y) \leftrightarrow z \leftrightarrow Z\)
がそれぞれ一対一に対応するので,正方形内の点 \((X, Y)\) の計数は \(\mathfrak{c}\) になる.
やり方はいろいろであろう.一例を示す.正方形は境界を含まないものとする.正方形の下側に頂点を持つ四角錐を作る.下図で青いのが正方形 \({\rm ABCD}\).真上から光を当てると考えて,正方形内の各点 \({\rm P}\) を \({\rm \triangle EAB,\, \triangle EBC,\, \triangle ECD,\, \triangle EDA}\) からなる側面(灰色部)に落とす.その点を \({\rm P'}\) とする.
次に,\({\rm ABCD}\) が平面と平行になるように立てる.正方形のまん中の点 \({\rm O}\) から \({\rm P'}\) を平面に投影する.\({\rm P \to P' \to P''}\) によって,正方形内の点と平面上の点が一対一に対応する.
1 次元の直線と 2 次元の平面を区別しないという意味.
直感的に明らかだが理由を付けておく.\({\rm M}\) を無限集合とし,その計数を \(\mathfrak{m}\) とする.\({\rm M}\) から順次要素を抜き出し \(\{m_1, \,m_2, \,m_3, \,\cdots \}\) という可符番無限の部分集合を作る.\({\rm M}\) を次のように2つに分ける.
\(\{m_1, \,m_2, \,m_3, \,\cdots \} + \{\text{左記以外の要素}\}\)
\(m_1, \,m_2, \,m_3,\,\cdots\) ですべて取り尽くしてしまい「左記以外の要素」がなければ,そこは空集合とする.\({\rm M}\) に新しい要素 \(\alpha\) をつけ加えた集合を \({\rm M'}\) とし,\({\rm M}\) から \({\rm M'}\) への対応を作る.
\(\{m_1, \,m_2, \,m_3, \,\cdots \}\) の部分では次のように要素を対応させる.
| \(m_1\) | \(m_2\) | \(m_3\) | \(m_4\) | … |
| ↓ | ↓ | ↓ | ↓ | |
| \(\alpha\) | \(m_1\) | \(m_2\) | \(m_3\) | … |
{左記以外の要素} があるなら,各要素に自分自身(正確には \({\rm M'}\) に属する自分の分身)を対応させる.
これで \({\rm M}\) から \({\rm M'}\) への一対一対応になるから,\(\mathfrak{m}+1=\mathfrak{m}\) である.
\(\mathfrak{M}\) はドイツ文字の M.この記法は,あとの章でも使われる.
現代の読者には \(\phi\) で通じるであろう.
一対一対応が存在したとして,\(a\in {\rm M}\) に部分集合 \({\rm S}(a)\in \mathfrak{M}\) が対応しているとする.
\(a \leftrightarrow {\rm S}(a).\)
あらゆる \(a\) について「\(a \notin {\rm S}(a)\) のときに限り \(a\in {\rm N}\)」として部分集合 \({\rm N}\) を作ればよい.本書で何度も出てくる記法で,合併集合 \({\rm A}\cup {\rm B}\) のことである.1952年当時の読者は集合の記号に通じていないので,わかりやすい「+」を用いたのだろう.
\({\rm A}\) と \({\rm B}\) が共通の要素をもたないときの合併集合を「直和」といい \(\mathrm{A\oplus B}\) などと書くことがある.3つ以上の集合でも,要素に重複がない場合に \(\mathrm{A\oplus B\oplus C}\) という具合に書く.
テキストには「\({\rm A}\) と \({\rm B}\) は共通の要素をもたない」とあるので,ここの \({\rm A+B}\) は「直和」と解釈する方がよいかもしれない.たしかに,第2章の途中までは「+」を「直和」と解釈するのが適切である.しかし,p.92 から先では「\(\cup\)」の意味で使われている.この記法が出てくるときは注釈を入れることにする.
テキストには定義が述べられていない.計数の乗法は次のように定義する.
集合 \({\rm M}\) の計数が \(\mathfrak{m}\),集合 \({\rm N}\) の計数が \(\mathfrak{n}\) のとき,\({\rm M}\) の要素と \({\rm N}\) の要素のペアからなる集合
\(\{(x,\,y)\,|\,x\in {\rm M},\,y\in {\rm N}\}\)
の計数を \(\mathfrak{m}\cdot \mathfrak{n}\) と定義する.
| p.46 | \(\mathfrak{m}\geqq \mathfrak{n}\) なら,\(\mathfrak{m}+\mathfrak{n}=\mathfrak{m}\quad \mathfrak{m}\cdot \mathfrak{n}=\mathfrak{m}\) |
結果が述べられているだけで,テキスト中に理由は書かれていない.
\({\rm A}\cap {\rm B}\) と同じ.少し前にある \(\mathfrak{m}\cdot \mathfrak{n}\) の記法とは無関係.
群論で文字が働きを表すことについては第 2 章に説明がある.ブール代数については,草稿段階では第 2 章の後半にあったのだと思う.あとからここに挿入した際,直し忘れたのだろう.
「この代数」とはブール代数のこと.