「演算」でもよい．その方がわかりやすいかもしれない．

1952年当時のことはよくわからないが，学校の科目であろう．「みなさんが学校で習った代数」という意味だと思う．

下にある対応表の左側を第一の対応，右側を第二の対応としている．

読み方は，群（ぐん）．あとにあるのは，環（かん），体（たい），束（そく）．

あなたの本で p.59 にある \(a_1\) 〜 \(a_6\) の定義と p.60 の左下にある \(a_3a_4\) の計算を見てほしい．
下の画像のようになっているなら問題はない．画像は第39刷（1986年11月10日発行）から撮影した．

もしも，次の画像のようになっているなら誤りである．この定義では p.61 の九九の表にならないし，\(a_3a_4\) の計算も間違っている．
こちらは第56刷（2007年10月5日発行）から撮影した．

図書館で調べてみると，

第17刷（1963年4月20日発行）
第21刷（1966年7月15日発行）
第31刷（1974年8月10日発行）
第36刷（1983年4月20日発行）
第39刷（1986年11月10日発行）

「もの」と「働き」については，pp.65-67 の具体例を読めば理解できると思う．単純な例としては，図形が「もの」であり回転や平行移動が「働き」となる．「働き」は何らかの作用であり，「もの」はその作用を受ける対象物であることが多い．

カントールの言葉（p.13 参照）．

表の右側に事実上同じ式が 2 度あって不審に思うかもしれない．はじめの式は \(a_2\) の逆元が \(a_3\) であることを意味し，2番目の式は \(a_3\) の逆元が \(a_2\) であることを意味している．

あたりまえすぎて意味がわからないかもしれない．はみ出す例を 2 つ示す．

・ \({\rm G}=\{0,\, 1,\,2\}\) とし、結合（演算）を通常の加法とする．\(1+2=3\) であり，\(3\) は \({\rm G}\) に属さない．つまり，\({\rm G}\) の外にはみ出している．

・ \({\rm G}\) をベクトルの集合とし，その内積を考える．このとき，\(\overrightarrow{\vphantom{b}a}\cdot \overrightarrow{b}\) は実数でありベクトルではない．つまり，\(\overrightarrow{\vphantom{b}a}\cdot \overrightarrow{b}\) は \({\rm G}\) の外にはみ出している．ベクトルの内積はなじみのある演算だが，本書で言うところの「結合」ではない．

単位元，逆元，結合法則についての補足説明をしておく．

単位元は，通常の乗法なら 1，加法なら 0 に相当するものである．
逆元は，通常の乗法なら \(x\) に対する \(1/x\)，加法なら \(x\) に対する \(-x\) である．

3つについて結合法則が成り立てば，いくつでも成り立つ．すなわち， \[\qquad [{(ab)c}d]e=[a{(bc)d}]e=a{(bc)(de)}=\cdots\] のようにどこから計算を始めても同じになる．よって，カッコをつけずに \(abcde\) と書いてかまわない．

ここから先，「要素」と書いたり「元（げん）」と書いたりしているが同じ意味である．

この式は，あらゆる元 \(a\) と固定された単位元 \(e\) について成り立つ．

次にある「（3）任意の元 \(a\) に対して … 逆元 \(b\) がある」の \(b\) は \(a\) ごとに異なる．

群の要素の個数のことを「位数」という．以後も「計数」と書いたり「位数」と書いたりしているので，覚えておく必要がある．

確認しておく．

整数と整数を加えたものは整数なので，

(1) \(a\in{\rm M},\, b\in{\rm M}\) ならば \(a+b\in{\rm M}\).

単位元は \(0\) で，すべての \(a\in{\rm M}\) について，

(2) \(a+0=0+a=a\).

\(a\in{\rm M}\) の逆元は \(-a\) であり，

(3) \(a+(-a)=(-a)+a=0\).

\(a,\,b,\,c\) が整数ならば，

(4) \((a+b)+c=a+(b+c)\).

(1)〜(4) により群の条件をすべて満たしている．

ここから「… 交換し合うことのできるものである（p.67）」までがひとまとまりである．説明を付けておく．

「位数 3 の群」の「九九の表」とは p.66 の左側の表のことである．\(a_1,\,a_2,\,a_3\) は p.59 のものと同じと考えてよい．この観点では \(a_1,\,a_2,\,a_3\) は「働き」と見なせる．そしてこの群をテキスト p.66 の下から 3 行目では \({\rm G}\) と呼んでいる（正確には p.61 の \({\rm G}\) の部分群であるがそのまま \({\rm G}\) としている）．

3個の要素 \(a_1,\,a_2,\,a_3\) に対して入れ換えを考える．入れ換えは「働き」であり，\(a_1,\,a_2,\,a_3\) は「働き」を受ける「もの」とみなす．これだけで「働き」が「もの」と考えられている例にはなっており，話は済んでいる．ここから先は，入れ換えのうち群論的に意味のあるものを考えるという副次的な話である．

\(b\) は \(a_2\) と \(a_3\) を入れ換えるという「働き」を表す．左側の「九九の表」の各項目で \(a_2\) と \(a_3\) を入れ換えたのが右側の表である．要素の並べ方が違うだけで実質的に同じ「九九の表」になっている．結合という関係性を壊さないこのような入れ換えによる自分自身への対応を p.58 にならって「同型」といっている．そのような入れ換えとして，

の 2 つがある（実はこの 2 つしかない）．この 2 つが群 \({\rm H}\) をつくり，その九九の表が p.67 の上にある．\({\rm H}\) を \({\rm G}\) の自己同型群という．

時々刻々の矢印の位置がわかれば，動き方の過程を含めてわかる．最後の位置だけなら，途中の動き方はもちろん不明である．

「あとで」は p.86 の「表現」のこと．

テキスト p.41 参照．

ここから 「… 数学特有の類別法はこのようなものである（p.76）」までが類別法の解説である．とくに理解しにくいところはないが，簡単なイメージを持ってもらうために，おおざっぱな説明をしておく．

学校のクラスでグループ分けを考える．先生が「好きな人とグループを作りなさい」と言ったとする．グループ分けにトラブルが発生する原因は次の 2 つである．

・ A さんは B さんが好きだが，B さんは A さんが好きではない．
・ A さんは B さんが好き，B さんは C さんが好き．しかし A さんは C さんが好きではない．

前者は「片思い」によるトラブル，後者は「友達の友達が友達とは限らない」ことによるトラブルである．

いま，あるクラスでこの2つの障害がないとする．すなわち，両思いの関係しかなく（対称的），友達の友達はまた友達（推移的）とする．この場合，グループ分けは円滑に行われる．

類別法とは，対称的・推移的（ここでは触れなかったがさらに反射的）な関係によって，関係のあるもの同士のグループを作ることである．

「＋」は「直和」と解釈するのが適切だろう．p.75 の \({\rm M}={\rm K}(a_1)+{\rm K}(a_2)+\cdots\cdots\) も同様．

対称的でないときは \(a \sim b \,({\small \rm R})\) と \(b \sim a \,({\small \rm R})\) の意味は異なる（A さんが B さんを好きと，B さんが A さんが好きは違う）．

文脈からわかるときは，単に \(a \sim b\) と書く（p.77 の一部でそうしている）．
なお，R は関係（Relation）にちなんだ文字．

テキストでは明記していないが，同値律を満たす 2 項関係のことを「同値関係」という．

わかりやすく区切ると次の通り．

「各要素の間に，ある “同値律をみたす 2 項関係 R” の規定されている」集合 M．

\(x \sim y\, ({\small \rm R}) \iff x \text{ と } y \text{ は同じ類}\)

これは同値律を満たす 2 項関係になる．この同値関係に基づいて数学的な類別を行うと，哺乳類，鳥類，… という具合にもとの類別が得られるということ．

「このようなもの」というのは p.70 からの説明全体を指しているのだろう．

数学的には剰余類がよい例なので参考までに説明しておく．

整数の集合を \({\rm M}\) とする．\({\rm M}\) の要素 \(x,\, y\) について，「\(x-y\) が \(3\) で割り切れる」を関係 \({\small \rm R}\) とする．

\( x \sim y \,({\small\rm R}) \iff x-y\) が \(3\) で割り切れる

これが同値関係であることを示そう．

\(x-x=0\) は \(3\) で割り切れるので \(x \sim x\, ({\small \rm R})\)．よって反射的．

\(x-y\) が \(3\) で割り切れれば，\(y-x=-(x-y)\) も \(3\) で割り切れるので，

\(x \sim y\, ({\small\rm R})\) ならば \(y\sim x\, ({\small \rm R})\).

よって対称的．

\(x-y\) と \(y-z\) が \(3\) で割り切れれば，\(x-z=(x-y)+(y-z)\) も \(3\) で割り切れるので，

\(x \sim y\, ({\small\rm R})\) かつ \(y\sim z\, ({\small\rm R})\) ならば \(x\sim z\,({\small \rm R})\).

よって推移的．

以上でこの関係が同値関係であることがわかった．

この同値関係で類別を行うと，\({\rm M}\) は，

（\(3\) で割り切れるもの） \( = \{\cdots,\, -6,\, -3,\, 0,\, 3,\, 6,\, \cdots\},\)
（\(3\) で割って \(1\) 余るもの）\( = \{\cdots,\, -5,\, -2,\, 1,\, 4,\, 7,\, \cdots\},\)
（\(3\) で割って \(2\) 余るもの）\( = \{\cdots,\, -4,\, -1,\, 2,\, 5,\, 8,\, \cdots\}\)

という 3 つの類に分かれる．これが剰余類である．

ここから「 … 割りきることがわかる（p.78）」までが証明になる．わかりにくいところが多いので解説する．

まず，いくつか基本的なことを証明しておく．

定理1.　群 \(\mathrm{G}\) の要素 \(a,x,y\) について，\(ax=ay\) ならば \(x=y\) である．

[証明] \(ax=ay\) に左から \(a^{-1}\) をかける． \begin{align*} \qquad a^{-1}(ax)&=a^{-1}(ay)\\ \qquad (a^{-1}a)x&=(a^{-1}a)y \quad\,\text{(結合法則)}\\ \qquad ex&=ey \quad\qquad\,\,\,\text{(逆元の定義)}\\ \qquad x&=y \quad\qquad \quad\text{(単位元の定義)}\,\,[証明終わり] \end{align*}

定理 1 は式から \(a\) を約すことができるという趣旨である．同様に \(xa=ya\) ならば \(x=y\) である．なお，\(ay=ya\) が成り立つとは限らないので，\(ax=ya\) から \(a\) を約すのは誤りである．

次の定理 2 と定理 3 は，テキストでは当然のこととして暗に仮定している．

定理2.　群 \(\mathrm{G}\) の単位元は 1 つしかない．

[証明] 背理法による．異なる単位元 \(e,\,e'\) があったと仮定する．
\(e\) は単位元なので \(ee'=e'\)．\(e'\) も単位元なので \(ee'=e\)．
よって， \[\qquad e'=ee'=e.\] これは \(e,\,e'\) が異なることに矛盾する．[証明終わり]

定理3.　群 \(\mathrm{G}\) の要素 \(a\) の逆元は 1 つしかない．

[証明] 背理法による．\(a\) の逆元として異なる \(x,\,y\) があったと仮定する．
\(x\) は \(a\) の逆元なので \(ax=e\)．\(y\) も \(a\) の逆元なので \(ay=e\)．
よって，\(ax=ay\)．定理 1 より \(x=y\)．
これは \(x,\,y\) が異なることに矛盾する．[証明終わり]

定理4.　群 \(\mathrm{G}\) のあるひとつの要素 \(a\) について \(ax=a\) ならば \(x\) は単位元である．

もともと単位元とは，すべての要素 \(a\in {\rm G}\) について \(ae=ea=a\) となるものとして定義された．\({\rm G}\) が群であるか不明ならばこれをすべての \(a\) について確認する必要がある．しかし，すでに群であることがわかっているなら，どれか 1 つの要素 \(a\) について \(ax=a\) ならば \(x\) は単位元と確定する．これが定理 4 の意味することである．

次に，部分群であるための条件を見ておく．\({\rm G}\) を群とし，\({\rm H}\) を \({\rm G}\) の部分集合とする．群 \({\rm G}\) の結合（演算）をそのまま使って \({\rm H}\) が群になるとき，\({\rm H}\) を \({\rm G}\) の部分群という．p.63 を参考にすれば，次の 4 条件が必要である．

(1) \(a\in {\rm H},\, b\in {\rm H}\) ならば \(ab\in {\rm H}\).
(2) \(e'\in {\rm H}\) があって，すべての \(a\in {\rm H}\) について \(ae'=e'a=a\) （単位元の存在）．
(3) \(a \in {\rm H}\) に対して \(ax=xa=e'\) となる \(x\in {\rm H}\) がある（逆元の存在）．
(4) \(a\in {\rm H},\, b\in {\rm H},\, c\in{\rm H}\) のとき，\((ab)c=a(bc)\)（結合法則）．

(1) は結合の結果が \({\rm H}\) の外にはみ出さないということで必須の条件である．(2) は \({\rm H}\) の内部で単位元としての役割を果たす要素があるということ．その要素は必ずしも群 \({\rm G}\) の単位元でなくてもよいかもしれないので \(e'\) と書いた．しかし，\(ae'=a\) ならば定理 4 により \(e'=e\) である．つまり，群 \({\rm G}\) の単位元が \({\rm H}\) に含まれる．\(e'=e\) であれば (3) は \(ax=xa=e\) となり，これを満たす \(x\) は群 \({\rm G}\) での逆元 \(a^{-1}\) しかない（定理 3 による）．最後の条件 (4) は不要である．\({\rm G}\) が群だから結合法則は保証されている．

以上のことから \({\rm H}\) が部分群である条件は，次の 3 つでよい．

(1) \(a\in{\rm H},\, b\in{\rm H}\) ならば \(ab\in {\rm H}\).
(2) \(e\in {\rm H}\).
(3) \(a\in {\rm H}\) ならば \(a^{-1}\in {\rm H}\).

これらを予備知識としてテキストに戻る．記号の使い方に注意が必要である．部分群は \({\rm H,\, K}\) など大文字で表すのが普通なのだが，テキストでは部分群を \(g\) とし，その要素を \(g_1,\,g_2\) としている．つまり， \[\qquad g=\{g_1,\,g_2,\,\cdots\}.\] \(g\) は要素ではなく集合であることに気をつけてほしい．テキストで定義された 2 項関係が反射的，対称的，推移的であることを説明した部分はわかると思う．なお，「反射律，対称律，推移律」ともいいテキストは混用している．ポイントとなるのは， \[\qquad e\in g,\,\,\, g_1^{-1}\in g,\,\,\, g_2g_1\in g\] のところで，これは上記の部分群の条件 (2)，(3)，(1) をそれぞれ使っている．

p.78 の部分に移る．\(g\) の位数を \(m\) とし， \(g=\{g_1,\,g_2,\,\cdots,\,g_m\}\) とする．\(g_1,\,g_2,\,\cdots,\,g_m\) はもちろん相異なる．
さて，\({\rm G}\) の要素 \(a\) をひとつ選んだとき，\(x \sim a\) となる \(x\) は \(x=ag_i\,\, (i=1,\, 2,\, \cdots,\, m)\) と表せる．それらを集めたものが \(a\) を含む類になる．したがって， \(a\) を含む類は， \[\qquad \{ag_1,\, ag_2,\,\cdots,\,ag_m\}\] である．これを \(ag\) と書くことにするのである（要素 \(a\) と 集合 \(g\) をかけているので，説明がないと意味不明である）． \[\qquad ag=\{ag_1,\,ag_2,\,\cdots,\,ag_m\}.\] \(a=e\) のときは，\(eg=g\) になる．

\(ag_1,\,ag_2,\,\cdots,\,ag_m\) は相異なる．なぜなら，定理 1 より「\(ag_i=ag_j\) ならば \(g_i=g_j\)」だから，対偶をとることで，「\(g_i\neq g_j\) ならば \(ag_i\neq ag_j\)」となるからである．したがって，どの類も要素の数は \(m\) 個である．テキストでは \(g_i \to ag_i\) という対応が一対一であるという言い方で説明している．

あとはテキストの通りで，類別法により， \[\qquad {\rm G}=g+a_1g+a_2g+\cdots\] とできる．最初の \(g\) は \(eg\) と書いてもよい．ここの「+」は「直和」と解釈するのが適切である．
これより \({\rm G}\) の位数は \(m\) の倍数になることがわかり証明が完了する．

色分けするとわかりやすいかもしれない．

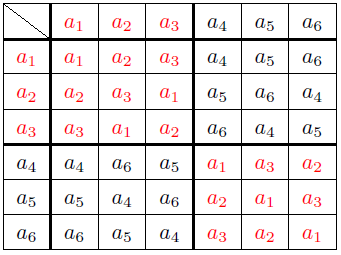
一方，p.80 にある \[\qquad {\rm K}_1=\{a_1,\,a_4\},\,\,{\rm K}_2=\{a_5,\,a_2\},\,\,{\rm K}_3=\{a_6,\,a_3\}\] の場合を色分けしたのが次の表．これは一団となって行動していない．

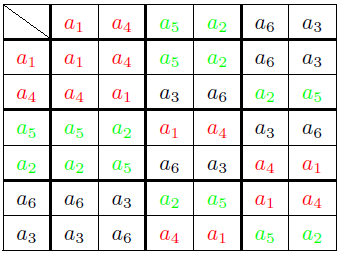
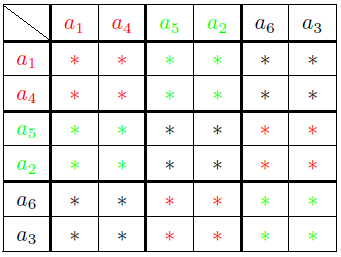
たとえば次の表のような色分けになれば一団となって行動していることになる．

ここから「… 写像は同型になるわけである（p.85）」までの内容は，一般の読者を対象とする読み物としてはやり過ぎだろう．「準同型定理」までを駆け足で説明しているのだが，もとから群論を知っている人以外はよくわからないと思う．本書を読み進めるのに必要ではないから読み飛ばしてよい．このあたりを知りたい場合は群論の入門書を読む方が早いはずである．

もちろん，\({\rm K_1}\) から 1 個，\({\rm K_2}\) から 1 個をそれぞれとってくるという意味．