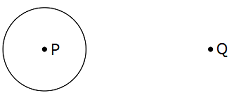
すべての点は平等であり,すべての直線も平等であるという意味.たとえば正方形からなる世界があったとする.その中央にある点 \({\rm P}\) と辺上の点 \({\rm Q}\) は平等ではない.辺上の点はいまにも落ちそうな崖っぷちにいる.数学的な違いとしては,\({\rm P}\) を中心とする円は存在するが,\({\rm Q}\) を中心とすると半円しか描けない.平等というのは周囲との関連において条件が同じということである.
任意の点 \({\rm P,\, Q}\) を選んだとき,ある射影変換で \({\rm P \to Q}\) となるものが存在する.これは変換式から計算で示すこともできるし,投影から考えてもよい.射影平面を \({\rm A}\),その複製を \({\rm A'}\)とする.\({\rm A'}\) 上の \({\rm Q}\) に相当する点を \({\rm Q'}\) とするとき,平面 \({\rm A}\) 上の点 \({\rm P}\) を平面 \({\rm A'}\) 上の点 \({\rm Q'}\) に写す投影が存在することは明らかである.
任意の直線 \(l\) を任意の直線 \(m\) に写す射影変換も存在する.複製した平面 \({\rm A'}\) 上の \(m\) に相当する直線を \(m'\) とするとき,平面 \({\rm A}\) 上の \(l\) と平面 \({\rm A'}\) 上の \(m'\) が重なるように平面 \({\rm A}\) と平面 \({\rm A'}\) を配置してから投影すればよい.
射影変換で写ることがなぜ平等を意味するのかの説明が少し難しい.
まず,ユークリッド幾何学で考える.通常の平面で 2 点 \({\rm P,\, Q}\) があるとする.点 \({\rm P}\) について,「点 \({\rm P}\) を中心とする円が存在する」という条件を考える.
点 \({\rm P}\) と円を丸ごと平行移動して \({\rm P}\) を \({\rm Q}\) に重ね合わせると,点 \({\rm Q}\) を中心とする円が存在することがわかる.ユークリッド変換で \({\rm P}\) が \({\rm Q}\) に写るなら,\({\rm P}\) を周囲との関連を含めて \({\rm Q}\) に重ね合わせることができるから,\({\rm P}\) と \({\rm Q}\) は平等といえるのである.
射影幾何学でまったく同じに「点 \({\rm P}\) を中心とする円が存在する」を考えるのは誤りになる.点 \({\rm P}\) と円を丸ごと射影変換して \({\rm P}\) を \({\rm Q}\) に写したとする.しかし,射影変換では「円」が「円」に写るとは限らない.これは「点 \({\rm P}\) を中心とする円が存在する」という条件を考えたのがおかしいのである.射影幾何学では射影変換で不変な性質を研究題目にするから,「円」についての条件を問題にすることはない.
射影変換で \({\rm P}\) が \({\rm Q}\) に写るならば,射影幾何学で問題になるような条件について,\({\rm P}\) と \({\rm Q}\) は平等といえる.つまり,射影幾何学的に \({\rm P}\) と \({\rm Q}\) は平等である.
神経質に解釈すれば,次のような意味になるだろう.
ある直線 \({\rm A}\) を選ぶ.\({\rm A}\) とは異なる任意の直線 \({\rm B,\, C}\) をとる.このとき適当な射影変換があって,
\[\qquad {\rm A \to A}\]
\[\qquad {\rm B \to C}\]
とできる(そのような射影変換が存在することの証明は省略する).
\({\rm A \to A}\) となる射影変換の全体 \({\rm G'}\) とする.\({\rm G'}\) によって不変な性質を調べる新しい幾何学ができる.\({\rm B \to C}\) であることは,その新しい幾何学において \({\rm A}\) 以外の直線が平等であることを示している.
次の 3 つを確かめればよい.\(a\circ b\) は写像の合成である.
(1) \(a\in {\rm G'},\, b\in {\rm G'}\) ならば \(a\circ b \in {\rm G'}\).いずれも該当する変換が \({\rm A \to A}\) をみたすことを確認すればよい.
(2) \({\rm G'}\) は単位元(恒等写像)を含む.
(3) \(a\in {\rm G'}\) ならば \(a\) の逆元(逆写像)も \({\rm G'}\)に含まれる.
同次座標 \([x,\, y,\, z]\) で示しておく.無限遠直線は \(z=0\) で表せる.
射影変換,
\begin{align*}
\qquad
\begin{cases}
x^\prime = a_{11}x+ a_{12}y+ a_{13}z\\[+3pt]
y^\prime =a_{21}x+ a_{22}y+ a_{23}z\\[+3pt]
z^\prime =a_{31}x+ a_{32}y+ a_{33}z
\end{cases}
\end{align*}
が無限遠直線を無限遠直線に写すとする.\(z=0\) であれば \(x,\, y\) に関わらず \(z'=0\) であればよい.よって,\(a_{31}=a_{32}=0\) である.このとき,
\begin{align*}
\qquad
D&=a_{11}a_{22}a_{33}+a_{13}a_{21}a_{32}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}\\
&=a_{11}a_{22}a_{33}-a_{12}a_{21}a_{33}\\
&=a_{33}(a_{11}a_{22}-a_{12}a_{21}).
\end{align*}
\(D\neq 0\) より,\(a_{33}\neq 0,\, a_{11}a_{22}-a_{12}a_{21}\neq 0\) である.射影変換は \(a_{ij}\) の連比できまるから,\(a_{33}\) で割ることで, \begin{align*} \qquad \begin{cases} x^\prime = ax+ by+ ez\\[+3pt] y^\prime =cx+ dy+ fz\\[+3pt] z^\prime =z \end{cases} \end{align*} と書ける.\(ad-bc\neq 0\) である.これが \({\rm G'}\) による変換式になる.
\({\rm G'}\) は無限遠直線上の点を無限遠直線上に写し,平面の有限部分の点を有限部分に写す.\({\rm G'}\) で不変な性質を調べるなら,平面の有限部分と無限遠直線を分けて考えてよい.テキストには明記されていないが有限部分だけで考えるのが普通である.
有限部分は \(X=x/z,\, Y=y/z\) により \(XY\) 平面とみなすことができ,そこでの変換式は, \begin{align*} \qquad \begin{cases} X^\prime= aX+ bY+ e\\[+5pt] Y^\prime= cX+ dY+ f \end{cases} \end{align*} となる.これはアフィン変換としてすでに紹介した(p.158の注釈).テキストでは「疑似」としているが,注釈では「アフィン」を使うことにする.
たとえば次図のように投影すればよい.平面 \({\rm A}\) からその複製 \({\rm A'}\) に \({\rm O}\) から投影する.\({\rm P}\) は 2 本の赤い直線の交点で,\({\rm O}\) は \({\rm OP}\) が平面 \({\rm A'}\) に平行になるようにとる.2本の赤い直線が青い平行線に写る.
逆写像を考えれば「平行な直線を平行でなくすること」もできる.
読み流してよいところだが,次の疑問を抱く人がいるかもしれない.
\({\rm G''}\) がユークリッド変換群になるという話らしい.結論を言うとこの 2 点は通常の無限遠点ではない.
しかし,無限遠点とは,ある特定の方向の遠くにある点だ.
回転で動かないわけがないじゃないか?
簡単に説明しておく.\(XY\) 座標でユークリッド変換を表したのが次の式. \begin{align*} \qquad \begin{cases} X^\prime = X\cos \theta \mp Y\sin \theta +a\\[+3pt] Y^\prime = X\sin \theta \pm Y\cos \theta+b \end{cases} \end{align*} 複号の上側をとると回転・平行移動を合成したもの,下側をとると対称移動が含まれ図形が裏返る.同次座標 \([x,\, y,\, z]\) でこれに対応する変換は次のようになる. \begin{align*} \qquad \begin{cases} x^\prime = x\cos \theta \mp y\sin \theta + az\\[+3pt] y^\prime =x\sin \theta\pm y\cos \theta+ bz\\[+3pt] z^\prime =z \end{cases} \end{align*}
無限遠直線上の 2 点 \({\rm I,\, J}\) を次のようにとる. \[\qquad {\rm I}=[1,i,0],\quad {\rm J}=[1,-i,0]\] \(i\) は虚数である.虚数であることは気にしないで上の変換式に代入して計算してみる.まず,複号の上側をとり,\({\rm I}\) の座標を代入する. \begin{align*} \qquad \begin{cases} x^\prime=\cos \theta-i\sin \theta\\[+3pt] y^\prime=\sin \theta+i \cos \theta=i(\cos \theta-i\sin \theta)\\[+3pt] z^\prime=0 \end{cases} \end{align*}
\(\lambda=\cos\theta-i \sin\theta\) とおくと,\([x',\, y',\, z']=[\lambda,\, \lambda i,\, 0]\) である.同次座標なので \(\lambda\) を約せば \({\rm I}\) と一致する.
同様に \({\rm J \to J}\) であり,\({\rm I,\, J}\) は不動点となる.
複号の下側をとると,\({\rm I}\) と \({\rm J}\) が入れ替わることがわかる.
虚数の使用を正当化するには,はじめから同次座標 \([x,\, y,\, z]\) の成分を複素数として一から理論をつくる必要がある.
テキストにある「無限遠直線上の 2 点」とは \({\rm I,\,J}\) のことである.射影変換のうち,この2点を動かさないか入れ替えるものは,正の定数 \(k\) を用いて, \begin{align*} \qquad \begin{cases} x^\prime = k(x\cos \theta \mp y\sin \theta + az)\\[+3pt] y^\prime =k(x\sin \theta\pm y\cos \theta+ bz)\\[+3pt] z^\prime =z \end{cases} \end{align*} と書けることが知られている.これが \({\rm G''}\) の変換式である.\(XY\) 座標の式に直すと,次のようになる. \begin{align*} \qquad \begin{cases} X^\prime = k(X\cos \theta \mp Y\sin \theta +a)\\[+3pt] Y^\prime = k(X\sin \theta \pm Y\cos \theta+b) \end{cases} \end{align*}
ユークリッド変換に \(k\) 倍の拡大を許したものなので,線分の比と角度を変えない.
意味のよくわからない表現である.先ほどの注釈の変換で \(k\) を任意の正の数とする.その場合,\({\rm G''}\) に従属する幾何学では,相似な図形を重ね合わせることができる.よって,相似な図形を同じと考える幾何学になる.
\(k=1\) に限定したものがユークリッド変換で,それに従属するのがユークリッド幾何学(普通の幾何学)である.
\({\rm G''}\) は上の注釈でいうと \(k=1\) としたもので,ユークリッド変換群であろう.
\({\rm G''\subset G'\subset G}\) となっており,それぞれの群で不変な性質を探求するのが各種の幾何学となる.ただし,アフィン幾何学とユークリッド幾何学は無限遠直線を切り離した通常の平面を対象とする.
| 変換群 | 名称 | 従属する幾何学 | 対象となる平面 |
| \({\rm G}\) | 射影変換群 | 射影幾何学 | 射影平面 |
| \({\rm G'}\) | アフィン変換群 | アフィン幾何学 | 通常の平面 |
| \({\rm G''}\) | ユークリッド変換群 | ユークリッド幾何学 | 通常の平面 |
p.164 の注釈で,上位の幾何学で成立する定理は下位の幾何学でも成立すると述べた.ここでもおおむねその通りだが,対象となる平面に微妙な違いがあるため,完全には成り立たない.たとえば,デザルグの定理(テキスト p.161)は射影幾何学では例外なく成り立つが,ユークリッド幾何学では例外が起こりうる.これについてはすでに述べた.
\(a_{ij}\) は射影変換の式に出てくる係数とは無関係である.誤解を招かないように, \[\qquad A_{11} x^2+2A_{12}xy+2A_{13}xz+A_{22}y^2+2A_{23}yz+A_{33}z^2=0\] などと書いた方がよいと思う.
復習しておくと,射影変換は, \begin{align*} \qquad \begin{cases} x^\prime = a_{11}x+ a_{12}y+ a_{13}z\\[+3pt] y^\prime =a_{21}x+ a_{22}y+ a_{23}z\\[+3pt] z^\prime =a_{31}x+ a_{32}y+ a_{33}z \end{cases} \end{align*} であり,これを \(x,\, y,\, z\) について解いた式が, \begin{align*} \qquad \begin{cases} x = a_{11}^\prime x^\prime+ a_{12}^\prime y^\prime+ a_{13}^\prime z^\prime\\[+3pt] y =a_{21}^\prime x^\prime+ a_{22}^\prime y+ a_{23}^\prime z^\prime\\[+3pt] z =a_{31}^\prime x^\prime+ a_{32}^\prime y^\prime+ a_{33}^\prime z^\prime \end{cases} \end{align*} である.
理解の助けになるかもしれないので,原理的にはこうすればよいという説明をする.
「ある一つの円」は単位円とする.同次座標での式は \(x^2+y^2-z^2=0\) である.変換式を代入すれば,
\[\qquad (a_{11}^\prime x^\prime+ a_{12}^\prime y^\prime+ a_{13}^\prime z^\prime)^2+(a_{21}^\prime x^\prime+ a_{22}^\prime y+ a_{23}^\prime z^\prime)^2-(a_{31}^\prime x^\prime+ a_{32}^\prime y^\prime+ a_{33}^\prime z^\prime)^2=0.\]
展開して,\(x',\, y',\, z'\) を \(x,\, y,\, z\) に書き換えると,
\[\qquad A x^2+B y^2+C z^2+Dxy+Eyz+Fzx=0 \]
の形になる.これが \(x^2+y^2-z^2=0\) と同じであるためには,
\[\qquad A=B=-C\neq 0,\,\,\,D=E=F=0\]
であればよい.これより \(a_{ij}'\) についてのかなり複雑な条件が出てくる.その複雑な条件を満たす変換の集合が \({\rm G'}\) である.\({\rm G'}\) は射影変換群 \({\rm G}\) の部分群になる.
なお,この条件では単位円が単位円に写るだけで,内部が内部に写るとは限らないと思うかもしれない.詳細は省くが,この条件だけで,
・ 円の内部 → 円の内部となる.内部と外部が入れ替わることはない.
・ 円周 → 円周
・ 円の外部 → 円の外部
射影平面を「円の内部」,「円周」,「円の外部」の 3 つに分けたとき,\({\rm G'}\) は,それぞれの部分の点をその部分の点に写す.よって,\({\rm G'}\) によって不変な性質を研究する際,この 3 つの部分を別々に考えてよい.ここでは内部のみを扱うということである.テキストは 2 次元の領域という意味で「内部と外部の 2 部分」としているが,次元にこだわらなければ「円周」を含めた 3 部分であろう.
以下,円の内部に非ユークリッド平面のモデルを作っていく.注釈ではこれを「円内モデル」と呼ぶことにする.正しくはベルトラミ-クライン・モデルという.
ユークリッド幾何学としての見方であろう.数学から離れると,地球に生命が誕生する以前から運動はあり,動いているものを同一のものと認識するように目や脳が進化した結果,私たちは長さという概念を獲得したのだろう.
第 3 章の書き方にならえば \(d\,({\rm P,\, Q})\) である.
直線上に \({\rm P,\, Q,\, R}\) の順に並んでいる必要がある.
\({\displaystyle a:b=\frac{a}{b}}\) という書き方をしている.
難しくないので証明をしておく.まず,複比が投影で不変なことを示す.
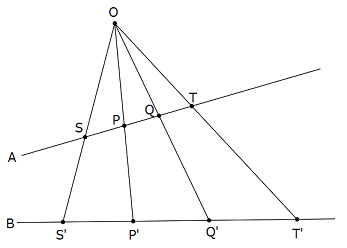
直線 \({\rm A}\) から直線 \({\rm B}\) に光源を \({\rm O}\) として投影をする.\({\rm O}\) から直線 \({\rm A}\) に下ろした垂線の長さを \(h\) とする.三角形の面積について, \[\qquad \bigtriangleup {\rm OPT}=\frac{1}{2}{\rm PT}\cdot h=\frac{1}{2}{\rm OP\cdot OT} \sin \angle {\rm POT}\] だから, \[\qquad {\rm PT}=\frac{{\rm OP\cdot OT}}{h}\sin \angle {\rm POT}.\] 同様にして, \[\qquad {\rm QS}=\frac{{\rm OQ\cdot OS}}{h}\sin \angle {\rm QOS},\] \[\qquad {\rm PS}=\frac{{\rm OP\cdot OS}}{h}\sin \angle {\rm POS},\] \[\qquad {\rm QT}=\frac{{\rm OQ\cdot OT}}{h}\sin \angle {\rm QOT}.\] これより複比は, \[\qquad {\rm \frac{PT\cdot QS}{PS\cdot QT}}=\frac{\sin \angle {\rm POT} \cdot \sin \angle {\rm QOS}}{\sin \angle {\rm POS}\cdot \sin \angle {\rm QOT}}.\] 同様にして, \[\qquad {\rm \frac{P'T'\cdot Q'S'}{P'S' \cdot Q'T'}}=\frac{\sin \angle {\rm P'OT'} \cdot \sin \angle {\rm Q'OS'}}{\sin \angle {\rm P'OS'}\cdot \sin \angle {\rm Q'OT'}}\] である. \[\qquad {\rm \angle {POT} = \angle {P'OT'},\,\, \angle {QOS}=\angle {Q'OS'},\,\,\angle {POS}=\angle {P'OS'},\,\,\angle {QOT}=\angle {Q'OT'}}\] であることから, \[\qquad {\rm \frac{PT\cdot QS}{PS\cdot QT}=\frac{P'T'\cdot Q'S'}{P'S' \cdot Q'T'}}.\] つまり,投影で複比は変わらない.
射影変換は複数の投影の合成から作られるので,射影変換で複比は不変である.
本来はテキスト p.107 の 4 条件を確認したいところである.
\(d\,({\rm P,\, Q})\) の記号を使えば,以下の 4 つである.
(1) \(d\,({\rm P,\, Q})\geqq 0 \)ここで定義した「距離」も,この 4 条件を満たしている.ただし,3 点が同一直線上にない場合に (4) を示すのはかなり難しい.
(2) \(d\,({\rm P,\, Q})=0 \iff {\rm P=Q}\)
(3) \(d\,({\rm P,\, Q})=d\,({\rm Q,\, P})\)
(4) \(d\,({\rm P,\, R})\leqq d\,({\rm P,\, Q})+d\,({\rm Q,\, R})\)
「角」が決まる理由を簡単に述べておく.1 点から等距離にある点の集合として「円」を描く.次に円に内接する 6 角形で辺の長さがすべて等しいものを描く.下図はユークリッド幾何学として描いたもの.赤丸をつけた角が 60°になる.正 360 角形を描けば 1°も作れる.
円内モデルに描き入れたのが次の図.私たちの目には歪んで見えるが,非ユークリッド世界の住人には,4 つとも同じサイズの「円」と「正 6 角形」であり,赤丸をつけた角はすべて「60°」である.
「小さくなることを注意しておこう」だと思う.「に」だと読者にもそれがわかるというニュアンスになるが,わかるわけがない.なお,内角の和は一定ではなく三角形ごとに異なる.
通常の平面上で円や線分を用い,その解釈を変えることで非ユークリッド幾何学のモデルを作ったことを指している.
変換群を先に決め,その変換で不変なものとして距離などを定義していく方法.「初めに群ありき(p.170)」の考え方.
球面世界の住人にとっての直線を「直線」と書くわけ.
それぞれの三角形のある場所の上空から見るということ.
ここから「… 左右反対になっていることを知るに違いない」までは正確な話になっていないので,できる限り精密にしてみる.球面上を考えるので,地球というよりシャボン玉のような球状の膜をイメージした方がよいだろう.
某君が住む世界が実在するとし,それをリーマン世界と名づける.球面上の 2 点を 1 点とみなしたものは,私たちが勝手に作り上げたリーマン世界のモデルにすぎない.実際のリーマン世界には,某君は 1 人しかいないし東京もひとつしかない.
さて,モデルにおいて某君が旧東京から新東京に行くならば,某君の分身は新東京から旧東京に行く.よって,2 人が出会うことはない.そして,本物の某君はリーマン世界を一周してもとの東京に戻ったのである.
そのとき某君は東京が左右反対になったと感じる.しかし,やがて某君は,東京はもとのままで自身の左右が逆になったことに気づくだろう.
ここのところも精密化する必要がある.リーマン世界は 2 次元なので,そこの住人はペシャンコの平面人間である.某君の実際の姿を次のようなものとする.
丸いところが頭で,右手と左手が生えている.右利きなので右手の方が太い.リーマン世界の住人が曲面にナメクジみたく貼り付いているとは思わないでほしい.面の表に貼り付いたナメクジと裏側に貼り付いたナメクジがお互い相手に気づかないまますれ違うことは 2 次元世界では起こりえない.彼らは面の「中」に存在している.
リーマン世界を一周した某君は,
となって東京に戻ってくる.リーマン世界にはメビウスの帯の構造が入っているためである.
どこで左右が入れ替わったのかという問いは無意味であり,世界を一周すると入れ替わる.私たちの地球における日付に似ている.現地時間に時計を合わせながら世界を一周すると日付がずれる.不便なので日付変更線を設けている.リーマン世界の住人も,どこかに「左右変更線」を設定し,そこを越えた瞬間に当人の左右が入れ替わると決めておくに違いない.
射影平面が球面上の 2 点を 1 点とみなしたものであることは,テキスト p.158 にある.
メビウスの帯が含まれることを示しておく.
球面の半分を考えたのが左側の図.テキストは北半球と南半球に分けていたが,ここでは縦割りにする.切り口の円周で,反対側にある 2 点を同じとみなす.理論的には,図の点線で結んだ 2 点がくっつくように円周を縫い合わせればよい.実際にやろうとするとグチャグチャになり,3 次元空間ではうまく実現できない.
赤道付近だけを考えたのが右側の図.この部分がメビウスの帯になることがわかるだろう.
円内モデルは,私たちから見ると長さや角度が不自然なものだった.何らかの曲面上で長さや角度が自然に見えるモデルがないかということである.
地球(正確には地球の表面の全世界)に対してメルカトル図法のような形が歪む地図がある.円内モデルはメルカトル図法に相当するもので,これに対する実物(数学的には不適当な用語だが)を知りたいのである.
(地球):(メルカトル図法)=(曲面 X ):(円内モデル)という関係にある曲面 X がないかということである.
曲面 X は理論的には存在する.しかし,その全体を 3 次元空間の中に実現することはできないことが知られている.そこで,多少妥協した形で示したのがテキストのラッパである.
筒状になる意味がわからないと思うので説明する.曲面 X の本来の姿は,どこまでも広がる面である.しかし,3 次元空間で曲面 X の全体を実現しようとするとシワシワになるところが出てきて,なめらかな曲面として描くことができない.そこで曲面 X の一部を切り取り示すことになる.
ちょうど平面の一部を切り取って円錐状にして示すようなことを曲面 X に対して行う.
切り取る部分を円内モデルで示したのが次の左図.曲面 X からこの部分に相当するところを切り出すと筒状に丸まった曲面になる.そこで PQ と PR に対応するところをくっつけたのが右図のラッパである.
頂点 P は無限遠にあるのでラッパはどこまでも細く伸びていく.赤い線から先を曲面として無理に実現しようとするとシワシワになってしまう.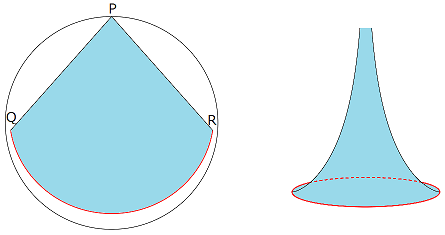
ラッパは曲面 X の一部を表したものにすぎないし,PQ と PR をくっつけたのでつながり具合も曲面 X と同じではない.また,テキストの図のようにラッパを 2 個つなげる必然性はなく,接合部分は正しいつながり方になっていない.
ここから「… 移動してしまうからである(p.184)」までは,はじめに曲線があると考えた方がわかりやすいだろう.
平面上に曲線があるとする.この曲線固有の性質とは,曲線の長さとか各点での曲率などである.
次のように座標を入れる.それぞれ \(y=f(x),\, y=g(x)\) と異なる関数で表せる.座標の入れ方によって極値の位置は変わるが,これは曲線固有の性質ではないからである.曲線の長さなどは,どちらの座標で計算しても変わらない.
\({\rm P}=(x,\, y)\) を原点中心に \(\theta^\circ\) 回転させ \({\rm P'}=(X,\, Y)\) とするのと,\({\rm P}\) を固定したまま座標を \(-\theta^\circ\) 回転させて \(XY\) 座標とするのは同じことである.
平行移動でも同様で,ユークリッド幾何学では図形を動かすのと座標を動かすのは同じことである.
アフィン幾何学や射影幾何学でも同様なのだが,そのためにはアフィン座標や射影座標の知識が必要になる.以下を読む上では,ユークリッド幾何学のイメージで理解すればよい.
3 点 \({\rm A} (x_1,\, y_1),\,\, {\rm B} (x_2,\, y_2),\,\, {\rm C} (x_3,\, y_3)\) の座標から三角形 \({\rm ABC}\) の面積を表す公式を作れば(面倒な式なので明示はしない),その式は(ユークリッド的な)座標変換で不変になる.
逆に,座標変換で不変な数式があれば,それは座標とは独立したその図形固有の性質(幾何学的な真実)を表わしているであろう.
こうすれば,あとに出てくる「もしある座標で書き表わした一つの方程式が … ある物理的な真実を表わしているはずではないか」の部分が理解しやすいと思う.
「不変式」は本書で初出の語.座標変換で変わらない式と理解すればよいのだろう.なぜ読者にとって未知の語を最後に書いたのかはわからない.もしかすると「不変量」の書き間違いかもしれない.