ガウス自身が私信の中で用いた言い回し.
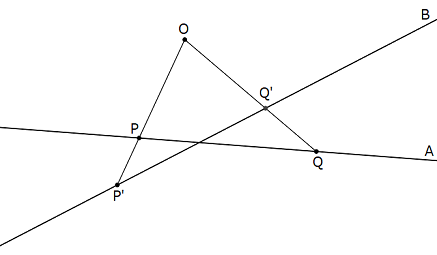
下図の \({\rm P \to P'}\) は光源による投影といってよいが,位置関係によっては \({\rm Q \to Q'}\) のように \({\rm O}\) の方向に引き戻す場合もある.
「投影は連続写像の一種」という意味.トポロジー的写像については p.122 参照.
このあたりは p.151 の図のように,無限遠点が関わってこない場合で考えている.
この章では,点にしろ直線にしろ,「写る」ではなく「変わる」「変化する」と言う.のちに扱う「変換」を運動と捉えて,点 \({\rm P}\) が移動して点 \({\rm Q}\) に「なる」という含みがあるらしい.注釈では「写る」を使う.
通常の平面に無限遠直線をつけ加えて射影平面にする話である.空間での図を書くのが難しいので,ここでは次元を下げて,通常の直線に無限遠点をつけ加えて射影直線にする話として説明しておく.\({\rm O}\) を光源とする直線 \({\rm A}\) から直線 \({\rm B}\) への投影を考える(下図).\({\rm L}\) がペーター・シュレミールで,写る先がない.直線 \({\rm A}\) のどの点も \({\rm M}\) に写ることはないので,\({\rm M}\) が幽霊である.
それぞれの平行線が無限遠点 \(\infty_{\rm A},\,\infty_{\rm B}\) で交わっていると考えればうまくいく.テキストの表現をまねれば,\(\infty_{\rm B}\) は「\({\rm B}\) の上に新しく点の影をつけ加え」であり,\(\infty_{\rm A}\) は「\({\rm A}\) の上に新しく点の肉体をつけ加え」である.
直線に無限遠点をつけ加えたものを「射影直線」という.射影直線「\({\rm A+\infty_{A}}\)」から射影直線「\({\rm B+\infty_{B}}\)」への投影は一対一写像になる.
イメージとしては平行線が無限遠で交わる.しかし,下図のように平行な 2 直線があるとき \({\rm P}\) と \({\rm P'}\) の 2 つの無限遠点があるとは考えない.交点は 1 つなので,\({\rm P=P'}\) とみなす.
直線の左の果て \({\rm P}\) と右の果て \({\rm P'}\) が一致すると考えるので,射影直線はつながり具合としては環状といえる.
だいたいのイメージを持ってもらうために,無理に熔接してみる.雑な話なので,あまり真面目に考えないでほしい.
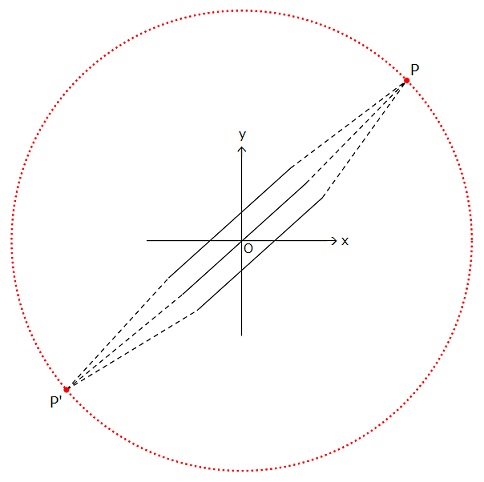
\(xy\) 平面があるとする.平面上の平行な直線は同一の無限遠点で交わる.図中において \({\rm P}\) と \({\rm P'}\) が無限遠点であるが \({\rm P=P'}\) である.これら無限遠点の集まりが無限遠直線となる.赤い点線の円として図示した.円の半径は無限大である.\({\rm P=P'}\) なので,1 つの点を 2 つに描いている.
ここから「… 無限遠点の解があると結論せねばならなくなった(p.156)」までは同次座標についての説明である.補足しておく.
「連比」という語が出てくるが,これは 3 つ以上の数の比のことである.
空間座標の点を \((x,\, y,\, z)\) で表し,連比で考える同次座標を \([x,\, y,\, z]\) と記すことにする.たとえば,\((1,\, 2,\, 3)\neq (2,\, 4,\, 6)\) だが \([1,\, 2,\, 3]=[2,\, 4,\, 6]\) である.\(x,\, y,\, z\) が \(x=y=z=0\) 以外のあらゆる実数をとるとき,\([x,\, y,\, z]\) からなる集合を \({\rm H}\) とし,個々の要素 \([x,\, y,\, z]\) のことを点と呼ぶことにする.結論としてはこれが射影平面と同一視できる.
\(t\) が \(0\) 以外の実数であれば \([a,\, b,\, c]=[ta,\, tb,\, tc]\) である.よって,1 つの点 \([a,\, b,\, c]\) に空間座標の 1 つの点 \((a,\, b,\, c)\) を対応させることはできない.1 つの点 \([a,\, b,\, c]\) には,原点を通る直線上の点 \((at,\, bt,\, ct)\) が対応する.
したがって,空間内にある無数の「原点を通る直線」を要素とする集合を \({\rm H}\) とみなすこともできる.その場合,その一つ一つの直線を「点」と呼んでいることになる.
空間内にある平面 \(z=1\) を考える.下図では青で示した.この平面に自然な \({XY}\) 座標を入れる.平面上の点 \((X,\, Y,\, 1)\) の座標を \((X,\, Y)\) とするのである.
原点を通る直線 \({\rm OP}\) と平面の交点を \({\rm P'}\) とする.\({\rm P}=(x,\, y,\, z)\) とし,\({\rm P'}\) を \(XY\) 座標で表すと, \[\qquad {\rm P'}=\left( \frac{x}{z},\,\frac{y}{z}\right)\] である.この対応で \({\rm H}\) の点 \([x,\, y,\, z]\) のうち \(z\neq 0\) であるものには,青い平面上の点 \({\rm P'}=(x/z,\, y/z)\) が対応する.そして,\(x,\, y\) を固定したまま \(z\) を \(0\) に近づければ,\({\rm P'}=(x/z,\, y/z)\) は無限の彼方へ飛び去っていく.このことから,青い平面に無限遠直線をつけ加えたものは \({\rm H}\) と同一視でき,無限遠点は \([x,\, y,\, 0]\) で表せることがわかると思う.
青い平面上の直線 \(aX+bY+c=0\) を考える.この直線上の点に対応する \({\rm H}\) の点 \([x,\, y,\, z]\) の満たすべき式は, \[\qquad a\left(\frac{x}{z}\right)+b\left(\frac{y}{z}\right)+c=0.\] 分母を払って, \[\qquad ax+by+cz=0\] となる.ただし,青い平面で考える限り \(z\neq 0\) の条件がつく.射影平面での直線の式は \(z\neq 0\) の条件を外せばよい.この直線と無限遠直線の交点を求めよう.無限遠直線は \(z=0\) で表せるので, \begin{align*} \qquad \begin{cases} \,\,ax+by+cz=0\\ \qquad\qquad\quad\,\,z=0 \end{cases} \end{align*} を解けばよい.\([b,\, -a,\, 0]\) となる.\([-b,\, a,\, 0]\) などとしてもよいが,同次座標なので \([b,\, -a,\, 0]=[-b,\, a,\, 0]\) である. \(c\) の値によらず同一の点で交わるので,平行な直線は同じ無限遠点を通る.
双曲線 \(XY=1\) でも同じ要領である.\((x/z)(y/z)=1\) の分母を払って, \[\qquad xy=z^2\] が射影平面での式となる.\(z=0\) とすると,\(x=0\) または \(y=0\) となる.よって,双曲線と無限遠直線の交点は, \[\qquad [0,\, y,\, 0],\,\,[x,\, 0,\, 0]\] となるが,同次座標では \([0,\, 1,\, 0]\) と \([1,\, 0,\, 0]\) に等しい.双曲線と無限遠直線は 2 点で交わる.
最後に単位円 \(X^2+Y^2=1\) について考える.\((x/z)^2+(y/z)^2=1\) の分母を払って, \[\qquad x^2+y^2=z^2\] が射影平面での式になる.無限遠直線との交点を求めるため \(z=0\) とすれば \(x^2+y^2=0\).\(x,\, y\) は実数なので \(x=y=0\) となる.\([0,\, 0,\, 0]\) は同次座標として定義されないので該当する点はない.単位円と無限遠直線は交わらないことになる.
微分積分学の基礎は実数論にあるため.高校までの数学では微分積分と \(\sqrt{2}\) の関連がわかりにくいかもしれない.
対蹠点(たいせきてん)とは,北極に対する南極のように球の真裏にある点のこと.
テキスト pp.179-181 参照.
「変換」とは集合 \({\rm M}\) から \({\rm M}\) 自身への一対一写像のことである.\({\rm M}\) を平面とすれば,平面上の点を別の点に写すので,点が移動すると解釈して「運動」ともいえる.
ここから先の話を理解しやすくするため,平面におけるユークリッド変換とアフィン変換について説明しておく.
ユークリッド変換とは,平行移動,回転,ある直線についての対称移動,およびこれらの変換を合成したものからなる.
\(xy\) 座標を用い \((x,\, y)\) が \((x',\, y')\) に写るすれば,次の式で表せる(式の詳細を理解する必要はない).
\begin{align*} \qquad \begin{cases} x^\prime = x\cos \theta \mp y\sin \theta +x_0\\[+3pt] y^\prime = x\sin \theta \pm y\cos \theta+y_0 \end{cases} \end{align*}\(x_0,\, y_0,\, \theta\) は定数で,複号同順である.ユークリッド変換では,長さや角度は変わらない.
アフィン変換を式で表したのが次の式.
\begin{align*} \qquad \begin{cases} x^\prime = ax+by+e\\[+3pt] y^\prime = cx+dy+f \end{cases} \end{align*}\(a,\, b,\, c,\, d\) は定数で \(ad-bc\neq 0\) の条件がつく.だいたいのイメージは下図のような変換である.
長さや角度は変わる.しかし,中点は中点に写るなど,同一直線上にある線分の比は変わらない.
正確に言うと,線分 \({\rm AB}\) を \(m : n\) に内分する点を \({\rm C}\) とする.これらがアフィン変換で写る点を \({\rm A',\, B',\, C'}\)とすると,\({\rm C'}\) は線分 \({\rm A'B'}\) を \(m : n\) に内分している.これは計算で容易に確認できる.
ユークリッド変換もアフィン変換も,変換の合成(ある変換のあとに次の変換を続けて行う)を結合(演算)として群を作る.群であることの確認は難しくないが,とくに必要ではないので省略する.
アフィン変換において, \[\qquad a=\cos \theta,\,\, b=\mp\sin \theta,\,\, c=\sin \theta,\,\, d=\pm\cos \theta,\,\, e=x_0,\,\, f=y_0\] とおけばユークリッド変換になる.つまりユークリッド変換はアフィン変換の特殊な場合である.したがって,ユークリッド変換群はアフィン変換群の部分群であり,集合として,
(ユークリッド変換群) \(\subset\) (アフィン変換群)である.
「特別な性質」とは,たぶん,「直線を直線に写す連続写像」のことであろう.
テキストは,ここから先の射影変換の定義がわかりにくい.
注釈では直線として図示するが \({\rm A,\,A'}\) は平面(正確には無限遠直線を含めた射影平面)である.
平面 \({\rm A}\) の複製を作り平面 \({\rm A'}\) とする.はじめにこの 2 枚の平面を重ねて,重ね合わせた位置は覚えておく.
2 枚をバラしたあと適当に配置して,次の図のように投影をする.
\({\rm P,\,P'}\) に印をつける.そして,はじめの重ね合わせ方と同じに,\({\rm A}\) と \({\rm A'}\) を重ねる.
これがひとつの投影から得られる射影変換である.
先ほどと同様に平面 \({\rm A}\) の複製 \({\rm A'}\) を作り,次の図のようにいくつかの投影を合成する.
テキストは 2 回の投影としているが,ここでは \({\rm O_1,\,O_2,\, O_3}\) を光源として,
\[\qquad {\rm P \to Q \to R \to P'}\]
の順に 3 回投影した.
\({\rm A}\) と \({\rm A'}\) をもとどおりに重ね合わせてできる \({\rm P \to P'}\) という変換も射影変換とする.
先ほどの 1 つだけの投影から作った変換とここの複数の投影から作った変換の両方が射影変換である.
テキストの方法とは異なるが,ここでは次のように射影変換を定義する.
定義 1. 1 つの投影から作った変換または複数の投影を合成して作った変換を射影変換という.
平面・直線はすべて無限遠点をつけ加えたもの,すなわち射影平面・射影直線のことである.1 つの投影から作った変換もしくは複数の投影を合成して作った変換(定義 1 による射影変換)が直線を直線に写すことは明らかであろう.
連続であることについては,無限遠点が関わらないとき,すなわち有限平面部分については納得がいくと思う.
しかし,無限遠点が絡むときは連続の定義が不明確である.本来はきちんとした取り扱いが必要なのだが,細かい話になるので省略する.定義 1 の射影変換が連続であることは容認しておく.
そして,テキストでは射影変換を次のように定義している.射影平面における一対一写像であることは前提とする.
定義 2. 直線を直線に写すような連続写像を射影変換という.
このような写像は,定義 1 における射影変換に限ることが知られている(証明はしない).よって,定義 1 と定義 2 のどちらで射影変換を定義しても同じである.
定義 2 を使い,だいたいの感じで理解すれば十分だろう.射影平面における連続性の定義が不明確なので,厳密に確認することはできない.
\(f,\, g\) を射影変換とするとき,その合成(\(f\) のあとに \(g\) を作用させる)を \(f \circ g\) と記す.普通の関数の記法では \(g(f(x))\) に相当する.射影変換の集合は合成を結合(演算)として群になる.このためには以下の 4 点を確認すればよい (p.63 参照).
(1) \(f,\, g\) が射影変換なら \(f \circ g\) も射影変換である.
(2) 恒等写像 (\(f(x)=x\) のように何も動かさない写像)が単位元になる.
(3) \(f\) が射影変換なら,その逆写像 \(f^{-1}\) が逆元になる.
(4) \(f,\, g,\, h\) が射影変換ならば,結合法則 (\(f \circ g ) \circ h=f \circ (g \circ h)\) が成り立つ.
(1) については,「連続性」と「直線が直線に写る」ことが合成で変わらないことによる.(4) の結合法則については射影変換に限らず一般の写像で成り立つ.
点 \({\rm P}\) に \(f,\, g,\, h\) を順に作用させて,\({\rm P \to P' \to P'' \to P^{\prime\prime\prime}}\) になるとする.
\[\qquad {\rm P} \xrightarrow{\quad f \quad} {\rm P'} \xrightarrow{\quad g\quad} {\rm P''} \xrightarrow{\quad h\quad} {\rm P^{\prime\prime\prime}}\]
このとき \(f \circ g\) をひとまとまりとして,
\[\qquad {\rm P} \xrightarrow {\quad f\circ g \quad} {\rm P''} \xrightarrow {\quad h\quad} {P^{\prime\prime\prime}}\]
と考えても,\(g \circ h\) をひとまとまりにして,
\[\qquad {\rm P} \xrightarrow{\quad f \quad} {\rm P'} \xrightarrow{\quad g\circ h \quad} {\rm P^{\prime\prime\prime}}\]
と考えても,全体としては \({\rm P}\) が \({\rm P^{\prime\prime\prime}}\) に写ることに変わりはない.よって,\((f \circ g) \circ h=f \circ (g \circ h)\) である.
基本となる変換式は,次の式である.
\begin{align*}
\qquad
\begin{cases}
x'= a_{11}x+ a_{12}y+ a_{13}z\\[+3pt]
y' =a_{21}x+ a_{22}y+ a_{23}z\\[+3pt]
z' =a_{31}x+ a_{32}y+ a_{33}z
\end{cases}
\end{align*}
一対一写像なので,これが \(x,\, y,\, z\) について解ける必要がある.そのため,
\[\qquad D=a_{11}a_{22}a_{33}+a_{13}a_{21}a_{32}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}\]
とするとき,\(D\neq 0\) が条件となる.連立 1 次方程式を解くだけではあるが,文字の数が多いので線形代数についての知識が必要であろう.詳細はわからなくてもかまわない.
\(D\neq 0\) であれば \(a_{ij}\) はどのような実数でもよい.\(x,\, y,\,z\) について解いた式を,テキストでは,
\begin{align*}
\qquad
\begin{cases}
x = a_{11}' x'+ a_{12}' y'+ a_{13}' z'\\[+3pt]
y =a_{21}' x'+ a_{22}' y+ a_{23}' z'\\[+3pt]
z =a_{31}' x'+ a_{32}' y'+ a_{33}' z'
\end{cases}
\end{align*}
とおいている.p.168 で利用したいため,ここで明示したようである.
同次座標に関連した注意をする.
射影平面上の点 \({\rm P}=[x,\, y,\, z]\) が射影変換で \({\rm P'}=[x',\, y',\, z']\) に写るとする.同次座標なので \(\lambda\neq 0\) を用いて \({\rm P}=[\lambda x,\, \lambda y,\, \lambda z]\) とも書ける.これを変換式に代入すると \([\lambda x',\, \lambda y', \lambda z']\) を得るが,同次座標では
\([x',\, y',\, z']=[\lambda x', \lambda y',\, \lambda z']\) なので同じ \({\rm P'}\) を表しており,話は整合している.
同様の理屈で \(a_{ij}\) をすべて \(\lambda a_{ij}\) に変えても \({\rm P'}\) は同じである.よって,射影変換の実質は \(a_{ij}\) の連比で決まる.
\([x,\, y,\, z]\) は \(X=x/z,\, Y=y/z\) とすれば,\(XY\) 平面上の点 \((X,\, Y)\) と同一視できるのだった(ただし \(z\neq 0\)).射影変換の式より, \[\qquad \frac{x^\prime}{z^\prime}=\frac{a_{11}x+ a_{12}y+ a_{13}z}{a_{31}x+ a_{32}y+ a_{33}z}=\frac{a_{11}(x/z)+ a_{12}(y/z)+ a_{13}}{a_{31}(x/z)+ a_{32}(y/z)+ a_{33}},\] \[\qquad \frac{y^\prime}{z^\prime}=\frac{a_{21}x+ a_{22}y+ a_{23}z}{a_{31}x+ a_{32}y+ a_{33}z}=\frac{a_{21}(x/z)+ a_{22}(y/z)+ a_{23}}{a_{31}(x/z)+ a_{32}(y/z)+ a_{33}}\] と書けるので, \begin{align*} \qquad \begin{cases} X^\prime={\displaystyle \frac{a_{11}X+ a_{12}Y+ a_{13}}{a_{31}X+ a_{32}Y+ a_{33}}}\\[+15pt] Y^\prime={\displaystyle \frac{a_{21}X+ a_{22}Y+ a_{23}}{a_{31}X+ a_{32}Y+ a_{33}}} \end{cases} \end{align*} と表せる.これが通常の \(XY\) 平面における射影変換の式である.右辺の分母が \(0\) になるときは無限遠点に写るとみなす.
次のような言い方とほぼ同じである.
同次座標において \([x,\, y,\, z]\) は連比で決まる.よって 3 個の文字を使っていても実質的には 2 個であり,2 次元の射影平面を表している.正確に説明するのは少し面倒だが,だいたいの意味はわかるであろう.
図形の性質のうち変わらないものという意味.「変わらない図形」の性質ではない.
「射影変換のうちのひとつであるところの投影」という意味.「特殊な射影変換である投影」「射影変換の一種である投影」でもよい.
「相対する頂点」とは,
\[\qquad {\rm A \leftrightarrow A',\quad B \leftrightarrow B',\quad C \leftrightarrow C'}\]
のこと.「相対する辺」も同様.
デザルグの定理は,通常の平面でもたいていは成り立つ.しかし,下図のような場合,3 つの交点は無限遠点になり,無限遠直線上にあるという意味で成立している.つまり,厳密には射影平面での定理である.
有名な定理であり証明はネットなどで探せば見つかる.
ユークリッドの『幾何学原論』第 1 巻にある定理 4 では「2 組の辺とその間の角がそれぞれ等しい 2 つの三角形は合同である(二辺夾角相等)」が述べられている.その証明として「片方の三角形をもう一方に重ね合わせるとピッタリ重なるから」という意味のことが書かれている(もちろんもっと正確な表現をしている).しかし,「重ね合わせる」という行為(運動)の定義は,『幾何学原論』の中のどこにもない.これは『幾何学原論』の欠陥とされている.
具体例で補足説明をする.
通常の平面で考える.変換群としてトポロジー的写像からなる群 \({\rm G}\),アフィン変換からなる群 \({\rm A}\),ユークリッド変換からなる群 \({\rm E}\) を考える.トポロジー的写像は,ゴム膜のように自由に伸び縮みするようなものとして,だいたいの理解でよい.あとの 2 つについては p.158 の注釈で説明した.
これら 3 つの群は \({\rm E\subset A\subset G}\) という関係にある.\({\rm E}\) によって不変な性質を調べるのがユークリッド幾何学,\({\rm A}\) によって不変な性質を調べるのがアフィン幾何学,\({\rm G}\) によって不変な性質を調べるのがトポロジーである.
ユークリッド幾何学とは,中学校で習う普通の幾何学のことである.
「長さ・角度」,「同一直線上の線分の比」,「閉曲線」という 3 つの概念にまつわる定理を見ていく.閉曲線とは下図のようにぐるりと 1 周した曲線のことで,円や楕円も閉曲線である.
「長さ・角度」にまつわる定理としてピタゴラスの定理がある.
「同一直線上の線分の比」にまつわる定理として,三角形の重心についての定理をとりあげる.三角形 \({\rm ABC}\) において,各頂点と対辺の中点を結んだ線分は 1 点で交わる.そして,下図で \({\rm AG:GM}=2:1\) である.これを重心定理と名づけておく.
「閉曲線」にまつわる定理としては, 「閉曲線は平面を内部と外部とに 2 分する」という定理がある(テキストp.121参照).これを閉曲線定理と名づけておく.
ユークリッド変換で「長さ・角度」,「同一直線上の線分の比」は不変である.「閉曲線」も形状をそのままに移動するだけなので,閉曲線という性質は不変である.したがって,これら 3 つの概念は,ユークリッド幾何学の研究題目になる.
ユークリッド幾何学では,ピタゴラスの定理,重心定理,閉曲線定理のいずれも成り立つ.
アフィン変換では,長さや角度は変わってしまう.「同一直線上の線分の比」は不変なので,これは研究題目になる.閉曲線は形状が歪んで円が楕円になることはあるが,閉曲線に変わりはない.よって,これも研究題目になる.
アフィン幾何学では,ピタゴラスの定理は意味を持たず,重心定理と閉曲線定理は成立する.
トポロジーに「長さ・角度」「比」という概念はない.閉曲線は形状が変わるものの,ぐるりと1周する性質は不変である.よって,閉曲線は研究題目になり,閉曲線定理のみ成立する.
以上を一覧表にした.
| 閉曲線定理 | 重心定理 | ピタゴラスの定理 | |
| トポロジー | ◯ | × | × |
| アフィン幾何学 | ◯ | ◯ | × |
| ユークリッド幾何学 | ◯ | ◯ | ◯ |
表の上方に位置する幾何学を上位の幾何学,下方にあるのを下位の幾何学ということにする.上位の幾何学で成り立つ定理は下位の幾何学でも成り立つ.ある変換群で不変な性質は,その部分群でも不変だからである.
そのため下位の幾何学になるほど概念が多種になり成立する定理は多くなる.しかし,閉曲線定理はトポロジーで扱うのがもっとも適している.ユークリッド幾何学では閉曲線の形状(円か楕円か)まで考慮しているが,それは不要なことである.重心定理はアフィン幾何学に適した定理であり,その三角形が正三角形か直角三角形かを問題にする必要はない.上位の幾何学は,少ない概念で定理の本質を突くという長所がある.
図形がちぎれてしまうのは容認しがたいという意味.
トポロジー的写像と同じ.