なじみのある例として，剰余類との関連に触れておく．通常の剰余類は加法と乗法の両方を扱うが，ここの話は加法に限定する．

5 で割った余りで整数を分け，それぞれの集合（剰余類）を \(\overline{0},\,\overline{1},\,\overline{2},\,\overline{3},\,\overline{4}\) とする．

\begin{align*} \overline{0}&=\{\cdots,\,-5,\,0,\,5,\,10,\,15,\,\cdots\},\\ \overline{1}&=\{\cdots,\,-4,\,1,\,6,\,11,\,16,\,\cdots\},\\ \overline{2}&=\{\cdots,\,-3,\,2,\,7,\,12,\,17,\,\cdots\},\\ \overline{3}&=\{\cdots,\,-2,\,3,\,8,\,13,\,18,\,\cdots\},\\ \overline{4}&=\{\cdots,\,-1,\,4,\,9,\,14,\,19,\,\cdots\}. \end{align*}

このとき，\(\overline{1}+\overline{2}\) を，それぞれから自由に要素を選んで足し合わせたものからなる集合と定義する．なお，ここの「＋」は「直和」や「\(\cup\)」とは無関係である．

{　} の中身は \(\overline{3}\) と同じなので， \[\qquad \overline{1}+\overline{2}=\overline{3}\] である．\(\overline{1}+\overline{3}\) とか \(\overline{3}+\overline{4}\) など他の場合も同様で，剰余類は加法について一団となって行動する．　 \[\qquad \mathrm{G}^\prime=\left\{\overline{0},\,\overline{1},\,\overline{2},\,\overline{3},\,\overline{4}\right\}\] とすると，\({\rm G'}\) は「+」を結合（演算）として位数 5 の群になる．

これは商群の一例になっている．整数全体の集合で加法を結合（演算）とした群を \({\rm G}\) とし，5 の倍数からなる集合を \(g\) とする． \[\qquad g=\{\cdots, -10,\,-5,\,0,\,5,\,10,\,\cdots\}.\] このとき，\(g\) は \({\rm G}\) の部分群で商群 \({\rm G}/g\) が \({\rm G'}\) になる．

ここから「… 商群のできることもすぐわかる（p.81）」までが，ひとまとまりである．

群 \({\rm G}\) の要素を部分群 \(g\) によって， \[\qquad a_1g,\,a_2g,\,a_3g,\,\cdots\] と類に分けたとき，これらの類の間に結合（演算）が整合的に定義できるための条件を調べる．

ここの意味がわかりにくい．まず，部分群 \(g\) の位数を \(m\) として，記号の意味などを説明する．\(g\) を有限群として説明するが，無限群でも同様である．

とし，\(g_1=e\) とする．群 \({\rm G}\) を部分群 \(g\) により類別する．\({\rm G}\) の要素 \(a\) を含む類は， \[\qquad ag=\{a,\,ag_2,\,ag_3,\,\cdots,\,ag_m\}\] であり，要素 \(b\) を含む類は， \[\qquad bg=\{b,\,bg_2,\,bg_3,\cdots,\,bg_m\}\] である．\(a\) と \(b\) が同じ類に属する場合は \(ag=bg\) である（クラスのグループ分けで \(a\) さんの友達を集めるとしても，\(b\) さんの友達を集めるとしても同じグループになる）．

\({\rm G}\) の要素 \(a,\, b\) について \(agb\) とは， \[\qquad agb=\{ab,\,ag_2b,\,ag_3b,\,\cdots,\,ag_mb\}\] のこととする（\(aeb=ab\) である）．\(b=a^{-1}\) のときは， \[\qquad aga^{-1}=\{e,\,ag_2a^{-1},\,ag_3a^{-1},\,\cdots,\,ag_ma^{-1}\}\] となる（\(aea^{-1}=e\) である）．

簡単な事実（逆元の逆元はもとの元）を定理として明記しておく．

定理5.　群 \({\rm G}\) の要素 \(a\) について， \[\qquad\qquad (a^{-1})^{-1}=a.\]

\(g\) は群なので，\(g^{-1}\) の要素はすべて \(g\) に属する．つまり，\(g^{-1}\subset g\)． また，\(g\) の任意の要素 \(g_k\) は，\(g_k=(g_k^{-1})^{-1}\) より，\(g\) に属するある要素の逆元だから，\(g\subset g^{-1}\) でもある．よって，\(g=g^{-1}\) となる．

群の部分集合同士のかけ算を定義したい．それぞれの集合から任意に要素を選んで群の結合（演算）によりかけ合わせたものの集合と定義する．
\(ag\) と \(bg\) をかけると，次のようになる．

右辺がひとつの類になるようにしたい．要素として \(ab\) があるので，それを含む類になるよりない． \[\qquad (ab)g=\{ab,\,abg_2,\,abg_3,\cdots,\,abg_m\}\] であるが， \[\qquad (ag)(bg)=(ab)g\] となるための \(g\) 条件を求めるのが，テキストのこの部分の目的である． \((ag)(bg)\) の要素は見かけ上 \(m^2\) 個あるので個数が合わないように思えるが，\(m^2\) 個の要素に重複があり，相異なるものが \(m\) 個ならば問題はない．

まず，\(b=a^{-1}\) という特殊な場合を考える．そのときの式が， \[\qquad (ag)(a^{-1}g)=g\] であり，テキストの 1 番目の式である．

ここで，\(gg^{-1}=g\) を示しておく．\(g^{-1}=g\) なので，

となる．\(g\) は群なので，この要素の中に \(g\) の外にはみ出すものはない．また 1 行目（あるいは 1 列目）にすべての \(g\) の要素が現れている．よって，\(gg^{-1}=g\) である．

以上で記号の意味はよいが，\(aga^{-1}=gg^{-1}=g\) の導出過程が不明である．ちょっと目には， \[\qquad (ag)(a^{-1}g)=g\] \[\qquad (aga^{-1})g=g\] として，両辺に右から \(g^{-1}\) をかけたように見える．しかし， \[\qquad (aga^{-1})\textcolor{red}{gg^{-1}}=gg^{-1}\] としても，\(g\) は集合であり要素とは違うので，赤くした部分を消すことはできない．

著者がどのように考えているのかはよくわからない．そこで，別の方法で \(aga^{-1}=g\) を示すことにする．これさえわかれば \(gg^{-1}=g\) と合わせて， \(aga^{-1}=gg^{-1}=g\) が成り立つことがわかる．

\((ag)(a^{-1}g)=g\) の左辺を明示したのが次の式．

1 列目に \(aga^{-1}\) の要素が現れているので，\(aga^{-1}\subset g\) である．\(a\) は \({\rm G}\) の任意の要素である．この結果と次の定理 6 により \(aga^{-1}=g\) を得る．

定理6.　群 \({\rm G}\) の任意の要素 \(a\) について \(aga^{-1} \subset g\) ならば，\(aga^{-1}=g\) である．

[証明] 任意の要素 \(a\) について \(aga^{-1}\subset g\) だから，\(a\) の代わりに \(a^{-1}\) を用いて， \[\qquad a^{-1}g(a^{-1})^{-1}\subset g\] が成立する．逆元の逆元はもとの元なので， \[\qquad a^{-1}ga\subset g.\] それぞれのあらゆる要素に，左から \(a\)，右から \(a^{-1}\) をかけることで， \[\qquad g\subset aga^{-1}.\] \(aga^{-1}\subset g\) と \(g \subset aga^{-1}\) の両方が成り立つので，\(aga^{-1}=g\) である．[証明終わり]

なお，定理 6 は，\(aga^{-1}\) と \(g\) の要素の個数がいずれも \(m\) 個であることから示すこともできる．しかし，その方法は無限群の場合に通用しない．

説明しておく．\(g\) を不変部分群とし，記号などは上の注釈のものをそのまま使う．
まず，\({\rm G}\) の任意の要素 \(a,\, b\) について， \[\qquad (ag)(bg)=(ab)g\] であることを示す．\(i,\,j\) を \(1,\, 2,\, …,\, m\) のいずれかの値としたとき， \[\qquad (ag_i)(bg_j)=abb^{-1}g_ibg_j=(ab)(b^{-1}g_ib)g_j\] と書けるから， \[\qquad (ag)(bg)=(ab)(b^{-1}gb)g\] である．右辺は，2 つの集合 \((b^{-1}gb)\) と \(g\) をかけて（すなわち，それぞれから勝手に要素を選びかけ合わせたものの集合を作って）から，各要素に \((ab)\) をかけるという意味である．

逆元の逆元がもとの元になることと \(g\) が不変部分群であることから， \[\qquad b^{-1}gb=(b^{-1})g(b^{-1})^{-1}=g.\] よって， \[\qquad (ag)(bg)=(ab)gg=(ab)g\] となる．\(gg=g\) であることはすでに示した．

これで，\({\rm G}\) の要素を \(g,\, a_1g,\, a_2g,\, \cdots\) と類に分けたとき，類の間のかけ算が整合的に定義できる． かけ算のルールは，それぞれの類から適当な要素を選びかけ合わせ，その結果が含まれている類が答である．
したがって，\(eg\,(=g)\) が単位元の役割を果たし，\(ag\) の逆元は \(a^{-1}g\) になる．また，\(a,\, b,\, c\) の間の結合法則から，\(ag,\, bg,\, cg\) の結合法則が成り立つ．

以上により，類をひと塊にしてひとつの要素とみなすと群になる．それを商群 \({\rm G}/g\) という．

一対一写像を \(f(a)=a'\) という具合に書くことにする．同型写像の条件は，\({\rm G}\) の任意の要素 \(a,\, b\) について， \[\qquad f(ab)=f(a)f(b)\] が成り立つことである．なお，\({\rm G}\) の結合（演算）を「\(\circ\)」，\({\rm G'}\) の結合を「\(\ast\)」と書くことにすれば， \[\qquad f(a\circ b)=f(a)\ast f(b)\] と書くのが正確である．

テキストでは，\({\rm G}\) の単位元を \(e\)，\({\rm G'}\) の単位元を \(e'\) と書いている．

「\(e\) が \(e'\) に写る」，「逆元が逆元に写る」は，\(f(ab)=f(a)f(b)\) の条件から自動的に成り立つ．これについては，あとの注釈で証明する．

本書で扱われる写像は，ほぼすべて一対一である．例外は pp.83-85 と pp.130-131 だけで，そこでは多対一を含めた写像を扱う．

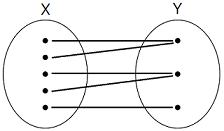
集合 \({\rm X}\) から集合 \({\rm Y}\) への写像を \(y=f(x)\) という具合に書くことにする（\(x\in {\rm X},\, y\in{\rm Y}\)）．写像とは，\({\rm X}\) 全体を定義域とする関数という理解でよい．その値域（\({\rm Y}\) のうち \(f(x)\) がとり得る部分）が \({\rm Y}\) 全体であるとき，その写像は「全射」であるという．簡単な例をあげる．

　[例1] \({\rm X,\, Y}\) を全実数からなる集合とするとき，\(y=x^2\) は \(y\) が負の値をとらないから全射ではない．
　[例2] \({\rm X}\) を全実数からなる集合，\({\rm Y}\) を 0 以上の実数からなる集合とすれば，\(y=x^2\) は全射である．

「多対一でもよい」とは「全射」と理解してよい．
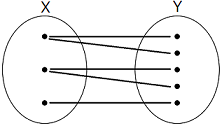
下図が「多対一でもよい」という写像である．1 つの \(y\) に対して， \(y=f(x)\) となる \(x\) が複数あってもよい．「複数でもよい」のであって，1 つでもかまわないことに注意．

下図の左側は全射でない例である．右側は「一対多」の場合だが，これはそもそも \({\rm X}\) から \({\rm Y}\) への写像と呼ばない．このような対応を本書で扱うことはない．

\({\rm G}\) から \({\rm G'}\) への写像を \(f(a)=a'\) という具合に表すと， \[\qquad f(ab)=f(a)f(b)\] という意味である．これが任意の \({\rm G}\) の要素 \(a,\, b\) について成立するとき，準同型写像という．

「単位元が単位元に写る」，「逆元が逆元に写る」を証明しておく．

\({\rm G}\) の単位元を \(e\)，\({\rm G'}\) の単位元を \(e'\) とする．このとき， \begin{align*} \qquad f(e)f(e)&=f(ee) \quad \text{（準同型写像の性質）}\\ &=f(e) \quad \,\,\, \text{（\(e\) は単位元なので \(ee=e\)）} \end{align*} \(f(e)=a'\) とおけば，\(a'f(e)=a'\) と書ける．定理 4（p.77の注釈）より，\(f(e)\) は \({\rm G'}\) の単位元とわかる．すなわち，\(f(e)=e'\)．これで単位元が単位元に写ることが示された．

次に，\({\rm G}\) の任意の元を \(a\) とする． \begin{align*} \qquad f(a)f(a^{-1})&=f(aa^{-1}) \quad \text{（準同型写像の性質）}\\ &=f(e) \quad\quad \,\,\,\text{（\(aa^{-1}=e\)）}\\ &=e^\prime \qquad \quad \,\,\,\, \text{（単位元は単位元に写る）} \end{align*} \(f(a)=a'\) とおけば，\(a'f(a^{-1})=e'\) となる．左から \((a')^{-1}\) をかけて，\(f(a^{-1})=(a')^{-1}\)．
つまり，\(a \to a'\) ならば \(a^{-1}\to (a')^{-1}\)．すなわち，\(a\) が \(a'\) に写るなら \(a\) の逆元は \(a'\) の逆元に写ることが示された．

次ページ図 (1) の通りだが， \[\qquad {\rm G}=\{a_1,\,a_2,\,a_3,\,a_4,\,a_5,\,a_6\},\quad {\rm G}^\prime=\{{\rm K}_1,\,{\rm K}_2\}\] であり， \[\qquad f(a_1)=f(a_2)=f(a_3)=\mathrm{K}_1,\] \[\qquad f(a_4)=f(a_5)=f(a_6)=\mathrm{K}_2\] という写像である．

\({e'}\) という要素だけからなる集合 \({\rm G'}=\{e'\}\) に \(e'e'=e'\) という結合（演算）を定義すれば，群の条件をすべて満たす．

そして，どのような群 \({\rm G}\) でも，すべての \(a\in {\rm G}\) について \(f(a)=e'\)と定義すれば，\({\rm G}\) から \({\rm G'}\) への準同型写像になる．

テキストには \({\rm G'}=\{e\}\) とあるが，これは \({\rm G}\) の部分群としての \(\{e\}\) を考えているためらしい．どちらで考えても差し支えない．

ここの類別は，同値関係から導かれる数学特有の類別法ではなく，生物学に似た類別法 (p.70) である．

\(G'=\{a',\, b',\, c',\, …\}\) とするとき， \begin{align*} \qquad &f(x)=a' \,\text{となるすべての } x \text{ からなる集合を }{\rm A},\\ &f(x)=b' \,\text{となるすべての } x \text{ からなる集合を }{\rm B},\\ &f(x)=c' \,\text{となるすべての } x \text{ からなる集合を }{\rm C},\\ & \qquad\qquad\quad\cdots\cdots \end{align*} とすれば， \[\qquad {\rm G}={\rm A+B+C}+\cdots\] とグループ分けができる．「＋」は「直和」と解釈するのが適切である．

写像は全射としているので，\({\rm A,\, B,\, C,\, \cdots}\) は空集合ではない．
作り方から，\({\rm A,\, B,\, C,\, \cdots }\) と \(a',\, b',\, c',\, \cdots\) は一対一に対応する．

テキストの説明の通りだが，\(f(a)\) などの記号で示しておく．
\({\rm G}\) から \({\rm G'}\) への写像を \(f(a)=a'\) という具合に書く．\({\rm G}\) の単位元を \(e\) とし，\({\rm G'}\) の単位元を \(e'\) とする．
\(g\) とは，\(f(x)=e'\) となるすべての \(x\) からなる集合である．

\(a\in g,\, b\in g\) とする．すなわち，\(f(a)=f(b)=e'\)． \begin{align*} \qquad f(ab)&=f(a)f(b) \quad \text{（準同型写像の性質）}\\ &=e^\prime e^\prime \\ &=e^\prime. \qquad\quad \,\,\,\text{（\(e'\) は単位元なので \(e' e'=e'\)）} \end{align*} よって， \(g\) の定義より \(ab\in g\) ．すなわち「\(a\in g,\, b\in g\) ならば \(ab\in g\) 」が成立する．

準同型写像は単位元を単位元に写すことはすでに証明した（p.83 の注釈）．
よって，\(f(e)=e'\) なので \(g\) の定義より \(e\in g\) ．

\(a\in g\) とする．準同型写像で「逆元が逆元に写る」ことはすでに証明した（p.83 の注釈）．
よって， \[\qquad f(a^{-1})=\{f(a)\}^{-1}.\] \(g\) の定義より \(f(a)=e'\) であり，\((e')^{-1}=e'\) なので， \[\qquad f(a^{-1})=e'.\] \(g\) の定義より \(a^{-1}\in g\) となる．すなわち「\(a\in g\) ならば \(a^{-1}\in g\) 」が成立する．

(1) \(a \in g,\, b\in g\) ならば \(ab\in g\).
(2) \(e\in g\).
(3) \(a\in g\) ならば \(a^{-1}\in g\).

\(g\) が不変部分群であることの定義は，
　「\({\rm G}\) の任意の要素 \(x\) に対して \(xgx^{-1}=g\) 」
だった．しかし，定理 6（p.81 の注釈）により，
　「\({\rm G}\) の任意の要素 \(x\) に対して \(xgx^{-1}\subset g\) 」
と定義してもよい．ここの部分は，著者も後者の定義で考えているように見える．以下，後者の定義で説明する．

テキストの言い方は，ベン図で示すと下図のような \(x\) が問題になることを強調している．

\(x\in g\) であれば，\(g\) が群であることから，\(xgx^{-1}\) が \(g\) の外にはみ出すことはない．したがって，\(xgx^{-1}\subset g\) は必ず成り立つ．よって，\(x\) が \(g\) に含まれない場合が問題になるのである．

しかし，単に「 \(x\) は \({\rm G}\) の任意の要素とする」でもよく，その方がわかりやすいだろう．

\(f(a)=a'\) という書き方で証明しておく．

\(x\in {\rm G},\, a\in g\) とする．

この部分はかなり飛躍があるので補足説明をする．

はじめに行った類別は生物学的なもので，\(g\) による類別と同じか不明である．同じであることを示す．
ここでの類別は， \begin{align*} \qquad &f(x)=a'\,\text{となるすべての } x \text{ からなる集合を }{\rm A},\\ &f(x)=b' \,\text{となるすべての } x \text{ からなる集合を }{\rm B},\\ &f(x)=c' \,\text{となるすべての } x \text{ からなる集合を }{\rm C},\\ & \qquad\qquad\quad\cdots\cdots \end{align*} という具合に決めたのだった（p.84 の注釈参照）．\({\rm A}\) がどのような集合か調べてみる．写像が全射であることから，\(f(a)=a'\) となる \(a\) が少なくともひとつある．そのとき， \begin{align*} \qquad x\in {\rm A} \iff & f(x)=a' \qquad\quad\,\,\,\,\,\,\text{（\({\rm A}\) の定義による）} \\ \iff & (a^\prime)^{-1}f(x)=e' \quad\,\, \text{（\(a'\) の逆元を左からかける）} \\ \iff & f(a^{-1})f(x)=e' \quad \text{（逆元は逆元に写るので \(f(a^{-1})\) は \(a'\) の逆元）} \\ \iff & f(a^{-1}x)=e' \qquad\,\,\, \text{（準同型写像の性質）} \\ \iff &a^{-1}x\in g \qquad\qquad\, \text{（\(g\) の定義による）} \\ \iff &x \in ag \qquad\qquad\quad\,\, \text{（左から \(a\) をかける）} \end{align*} となる．よって，\({\rm A}=ag\) である．これより，\({\rm A,\, B,\, C,\, \cdots}\) は \(g\) による類別と同じとわかる．

したがって，\({\rm A,\, B,\, C,\, \cdots}\) は商群 \({\rm G}/g\) の要素とみなしてよい．これらが \({\rm G'}\) の要素と一対一に対応することは p.84 の注釈ですでに述べた．\(a\) を含む類 \({\rm A}\) は \(f(a)=a'\) に対応し，\(b\) を含む類 \({\rm B}\) は \(f(b)=b'\) に対応する．\({\rm G}/g\) における積 \({\rm AB}\) は \(ab\) を含む類であり，それは \(f(ab)=f(a)f(b)=a'b'\) に対応する．

読み流してよいところだが「表現」の例として注釈を入れておく．
行列（マトリックス）の計算は既知とし，次のようにおく．

このとき「九九の表」は，テキスト p.61 の表と同じになる．このような九九の表を持つ群のひとつの具体例が p.59 にある 3 つの数字の入れ換えだが，もうひとつが上記の行列表現である．

\(\omega=\{1,\, 2,\, 3,\, \cdots \}\) と考えて差し支えない．

「ときも」というのは，大小関係の記号を流用するという意味であろう．もちろん，併用するわけではなく，ここでは「割り切れる」の意味だけで使う．
なお， \(a\) は \(a\) で割りきれるので，のちの記号の使い方との整合性からは「 \(\leqq \) 」である．ここでは「\(b\) が \(a\) で割りきれるが，\(a=b\) ではない」ときを「\(a \lt b\)」としているのだろう．

テキスト p.41 参照．

\(a\) は \(a\) の部分集合だから「 \(\geqq\) 」が正確である．ここでは「\(b\) が \(a\) の部分集合だが，\(a=b\) ではない」ときを「\(a \gt b\)」としているのだろう．

もちろん，どの要素の間にも関係があるわけではない．
また，\(x\geqq y\) ではあるが \(x=y\) でないときを \(x \gt y\) と記す（以下でそのような使い方をしている）．

「これ」とは \(a\) と \(c\) を直接に結ぶ線のこと．

図中の {　} は空集合のこと．

「このような集合」とは「集合 \({\rm M}\) のすべての部分集合の集合 \(\mathfrak{M}\)」のことで，テキスト p.41 で説明されている．

「合併集合」は p.44 で定義している．そこでは共通の要素を持たないとしていたが，ここでは共通の要素があってもよい．\({\rm A\cup B}\) のことである．

「共通集合」は p.46 で定義している（ただし共通部分と呼んでいた）．\({\rm A\cap B}\) のことである．

\({\rm A+B}\) は \({\rm A\cup B}\) の意味．やろうとしていることは，すでに知っている \({\rm A+B}\) を順序を使って定義し直したいのである．

この注釈では「\(\leqq\)」の代わりに「\(\subset\)」を使うことにする．

\({\rm A,\, B,\, C}\) はすべて \(\mathfrak{M}\) の要素，すなわち「集合 \({\rm M}\) の部分集合」である．「大きい」「小さい」は包含関係のことで，\({\rm A \subset B}\) なら「\({\rm B}\) は \({\rm A}\) より大きい」，「\({\rm A}\) は \({\rm B}\) より小さい」という．「大きい」「小さい」に等号が含まれていることに注意．「大きいか等しい」「小さいか等しい」とすれば正確である．

\({\rm A\subset C}\) かつ \({\rm B\subset C}\) となるあらゆる \({\rm C}\) を考える．それを， \[\qquad \{{\rm C_1,\,C_2,\,C_3,\,C_4,\,\cdots}\}\] としよう．この中で，たとえば \({\rm C_1}\) が一番小さいとは， \begin{align*} \qquad {\rm C_1}&\subset {\rm C_2},\\ {\rm C_1}&\subset {\rm C_3},\\ {\rm C_1}&\subset {\rm C_4},\\ &\cdots \end{align*} がすべて成り立つことをいう．半順序系を考えているので，どの 2 つの要素間にも大小関係があるわけではない．しかし，「一番小さいもの」とは，\({\rm C_2,\, C_3,\, C_4,\, \cdots}\) のすべてと関係を持った上で小さいことをいう．

実際，\({\rm A,\, B}\) のいずれも含む部分集合の中で \({\rm A∪B}\) が一番小さいことは，ベン図で考えればすぐにわかる．

読者が集合の記号に通じていないことを前提にしている．現代の読者向けには， \[\qquad {\rm A\vee B,\,\,\, A\wedge B}\] などと書いた方がよい．\(\mathfrak{M}\) に包含関係で順序を入れて，

\({\rm A\vee B = A,\, B}\) の両方より大きいものの中で一番小さいもの
\({\rm A\wedge B = A,\, B}\) の両方より小さいものの中で一番大きいもの

ここから「 … 共通の子孫もないはずである（p.93）」までがひとまとまりである．子孫関係による半順序系では，\({\rm A\cup B,\,A\cap B}\) が存在するとは限らないことを説明している．

\({\rm A}\) が \({\rm B}\) の子孫であるとき \({\rm A\leqq B}\) と定義する（子孫に自分自身も含めるので日常語の “子孫” とは少し意味が違う）．

たとえば \({\rm A}\) が \({\rm B}\) の父親ならば \({\rm A\cup B=A}\) になる．\({\rm A}\) と \({\rm B}\) の両方の祖先とは \({\rm A}\) の祖先（\({\rm A}\) 自身を含む）と一致し，\({\rm A}\) は，その祖先たちのどの人から見ても子孫だからである．このように \({\rm A\cup B}\) が存在する場合もある．

しかし，一般には \({\rm A\cup B}\) は存在しない．共通の祖先がいない場合はもちろんだが，共通の祖先がいたとしても \({\rm A\cup B}\) が存在するとは限らない．これは次の兄弟の例からわかる．

\({\rm A}\) と \({\rm B}\) が兄弟とする．共通の祖先とは，父方の祖先と母方の祖先を合わせた全員である．この全員からなる集合を \({\rm X}\) とする．\({\rm X}\) には父親，母親は含まれているが \({\rm A,\,B}\) は含まれていない．\({\rm A\cup B}\) とは，\({\rm X}\) の中で，\({\rm X}\) のどの人から見ても子孫という人物である．これは存在しない．そのような人物は父親と母親の子孫でなくてはならないが \({\rm A,\, B}\) は \({\rm X}\) に含まれていないからである．ただし，父親が母親の息子であるという異常な場合（父親がギリシア神話のエディプスのような場合）は，その父親が \({\rm A\cup B}\) となる．

テキストにある「二人の子供 \({\rm A,\, B}\) の間には \({\rm A\cap B}\) は決して存在しない」の理由はよくわからない．近親婚が許されないので共通の子供はいないだろうが，何世代かたてば共通の子孫が現れてもおかしくないし，\({\rm A\cap B}\) が存在することもあり得るはずである．もちろん，存在しない場合もあるので「存在するとは限らない」は正しい．

厳密には「空集合以外の部分集合をとると」である．

ていねいに書けば「\(\omega\) のどのような部分集合（ただし空集合は除く）をとってもその部分集合に最小の要素がある」．

帰納法との関連については，テキスト p.96 の「部分集合といっても，少なくとも一つの要素は … 一番小さい番号 \(m\) がある」を参照．まだ示していない部分に最小があるから，それを「次の一つ」として帰納法が成り立つ．

これに帰納法を適用しても永久に \(1'\) に到達しないと思うかもしれない．

帰納法は次の2つのステップからなる．

(I) \(n=1\) について示す．
(II) ある部分で成立したら次の一つも成立する．

(a) \(1,\, 2,\,\, \cdots ,\, n\) で成立したら \(n+1\) でも成立．
(b) \(1,\, 2,\,\, \cdots\cdots\) で成立したら \(1'\) でも成立．
(c) \(1,\, 2,\, \cdots\cdots,\, 1',\, 2',\, \cdots,\, n'\) で成立したら \((n+1)'\) でも成立．