数学では，直線は 1 次元の空間，平面は 2 次元の空間とする．

平面全体の点の計数が \(\mathfrak{c}\) であることは，テキストp.39 にある．
立体については書かれていない．3 次元空間全体の場合なら，たとえば次のようにすればよい．
平面全体の点の計数が \(\mathfrak{c}\) なので，実数 \(w\) と， \[\qquad (x,\, y) \leftrightarrow w\] という一対一対応が存在する．よって． \[\qquad (x,\,y,\,z) \leftrightarrow (w,\, z)\] が一対一に対応する．\((w,\, z)\) は平面全体の点と見なせるので計数は \(\mathfrak{c}\) である．

立方体ならば，\(0\lt x,\, y,\, z,\, w \lt 1\) として，正方形内の点の計数が \(\mathfrak{c}\) であることから同様に示せる．

平面上の点を \({\rm P}=(x,\, y)\) と記すように，直線上の点を \({\rm P}=(x)\) と記している．

\(d\) は距離（distance）の意．

「可符番」については p.21 を参照．

あらゆる点についての条件である．つまり，上記の \(d\,({\rm P,\,P'})\) の例ならば， \[\qquad x_1^2+x_2^2+\cdots\cdots+x_n^2+\cdots\cdots,\quad x_1^{\prime\, 2}+x_2^{\prime\, 2}+\cdots\cdots+x_n^{\prime\, 2}+\cdots\cdots\] のいずれも有限であることが条件である．このとき \(d\,({\rm P,\,P'})\) も有限になることが知られている．

もちろん「いろいろな種類の空間」「多様な空間」という意味．

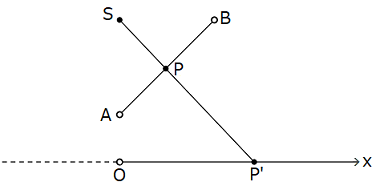
平面上の円は，中心の座標 \((x,\, y)\) と半径 \(r\) で決まる．\(r \gt 0\) であるが，正の実数の計数は線分（端点は除く）上の点の計数と同じである．なぜなら，次図において，線分 \({\rm AB}\) と数直線の正の部分は定点 \({\rm S}\) からの投影 \({\rm P \to P'}\) で一対一に対応するからである．\({\rm S}\) は，\({\rm SB}\) が数直線に平行で，\({\rm S,\, A,\, O}\) が一直線上にあるようにとる．

よって，正の実数からなる集合の計数は \(\mathfrak{c}\) である．

「正の実数 \(r\)」と「正・負・ゼロを含めた実数 \(z\)」の計数はどちらも \(\mathfrak{c}\) なので \(r \leftrightarrow z\) という一対一対応が存在する．したがって， \[\qquad (x,\, y,\, r) \leftrightarrow (x,\, y,\, z)\] により \({\rm R}\) の要素は 3 次元空間全体の点と一対一に対応する．よって，p.103 の注釈より \({\rm R}\) の計数は \(\mathfrak{c}\) になる．

示すべき式は \(d\, ({\rm P,\, P'})+d\,({\rm P',\, P''})\geqq d\,({\rm P, P'')}\) である．これ以外の条件は易しい．
図を描いて理解すれば十分と思われるが，ここでは記号的に示しておく．

\({\rm P}\) で円の周または内部の点の集合を表すことにする．\({\rm P\cap P'}\) などは通常の集合の記号である．\(\overline{\rm P}\) は補集合を表し，円の外部とする．
集合 \({\rm X}\) の面積を \(S({\rm X})\) で表す．\({\rm X}\) が 1 点からなる場合や空集合の場合は \(S({\rm X})=0\) とする．

ここで定義されている距離は， \[\qquad d\,({\rm P,\,P'})=S(\,{\rm P \cap \overline{P'}}\,)+S(\,{\rm \overline{P} \cap P'}\,)\] と表せる． \[\qquad {\rm P \cap \overline{P'}\supset P \cap \overline{P'}\cap \overline{P''}},\quad {\rm \overline{P} \cap P' \supset \overline{P} \cap P'\cap P''}\] であり，一般に \({\rm X \supset Y}\) ならば \(S({\rm X})\geqq S({\rm Y})\) なので， \[\qquad d\,({\rm P,\,P'})\geqq S(\,{\rm P \cap \overline{P'}\cap\overline{P''}}\,)+S(\,{\rm \overline{P} \cap P'\cap P''}\,).\] この式で \({\rm P}\) と \({\rm P''}\) を入れ替える． \[\qquad d\,({\rm P'',\,P'})\geqq S(\,{\rm P'' \cap \overline{P'}\cap\overline{P}}\,)+S(\,{\rm \overline{P''} \cap P'\cap P}\,).\] 2 式を加える．\({\rm X\cap Y\cap Z}\) は \({\rm X,\, Y,\, Z}\) の順序によらないことと \(d\,({\rm P'',\,P'})=d\,({\rm P',\,P''})\) から，次のように整理できる． \[d\,({\rm P,\,P'})+d\,({\rm P',\,P''})\geqq\left\{S(\,{\rm P \cap \overline{P''}\cap\overline{P'}}\,)+S(\,{\rm P \cap \overline{P''}\cap {P'}}\,)\right\}+\left\{S(\,{\rm \overline{P} \cap P'' \cap \overline{P'}}\,)+S(\,{\rm \overline{P}\cap P'' \cap P' }\,)\right\}.\] 一般に \(S({\rm X\cap \overline{P'}})+S({\,\rm X\cap P'\,})=S({\rm X})\) である．なぜなら，左辺は \({\rm X}\) の面積を \({\rm P'}\) の外部と内部に分けて加えたものだからである．
上の式にこれを適用すれば， \[\qquad d\,({\rm P,\,P'})+d\,({\rm P',\,P''})\geqq S(\,{\rm P \cap \overline{P''}}\,)+S(\,{\rm \overline{P} \cap P'' }\,).\] 右辺は \(d\,({\rm P,\,P''})\) であり，これが示すべき式であった．

\(0\leqq x\leqq 1\) のこと．通常は \(0\lt x\lt 1\) だが，あとの文脈から端点を含めていると思われる．

\({\rm P,\, P'}\) を \(f(x),\, g(x)\) のこととする．\(d\,({\rm P,\, P'})\) とは，\(|f(x)-g(x)|\) の \(0≦x≦1\) における最大値である．
記号で書くなら， \[\qquad d\,({\rm P,\,P'})=\max_{0\leqq x \leqq 1} {|f(x)-g(x)|}.\] \(0\lt x\lt 1\) とすると最大値が存在しない可能性があるので \(0\leqq x\leqq 1\) であろう．

4 条件とは p.107 の (1)〜(4)，あるいは p.113 の (2)〜(5) のこと．
\(d\,({\rm P,\, P''})\leqq d\,({\rm P,\, P'})+d\,({\rm P',\, P''})\) を示しておく．他の条件は易しい．

\({\rm P,\, P',\, P''}\) を \(f(x),\, g(x),\, h(x)\) のこととする．\(|f(x)-h(x)|\) は \(x=x_0\) で最大になるとすると， \[\qquad d\,({\rm P,\,P''})=|f(x_0)-h(x_0)|.\] \(f(x_0)-h(x_0)=\{f(x_0)-g(x_0)\}+\{g(x_0)-h(x_0)\}\) に，実数における三角不等式 \(|a+b|≦|a|+|b|\) を適用して， \[\qquad d\,({\rm P,\,P''})\leqq |f(x_0)-g(x_0)|+|g(x_0)-h(x_0)|.\] \(d\,({\rm P,\, P'}),\, d\,({\rm P',\, P''})\) は，それぞれ \(|f(x)-g(x)|,\, |g(x)-h(x)|\) の最大値なので， \[\qquad |f(x_0)-g(x_0)|\leqq d\,({\rm P,\,P'}),\quad |g(x_0)-h(x_0)|\leqq d\,({\rm P',\,P''})\] である．これらの式より，\(d\,({\rm P,\, P''})\leqq d\,({\rm P,\, P'})+d\,({\rm P',\, P''})\) がわかる．

\(0\leqq x\leqq 1\) で連続な関数 \(f(x)\) の研究をしている解析学者が，それを「点」とみなしたとする．その「点」を \(0\leqq x \leqq 1/2\) と \(1/2\leqq x\leqq 1\) の部分に分けることはできないのだろうか？ その解析学者の目下の研究にとっては \(0\leqq x\leqq 1\) 全体で考えた方がよく，分ける意味がないのである．

先を読めばわかるが輪ゴムをイメージすればよい．円板ではない．

集合 \({\rm M}\) から \({\rm M'}\) への写像を，\(x'=f(x)\,\,\, (x\in{\rm M},\, x'\in{\rm M'})\) という具合に書くとする．
このような記号と「連続」という言葉の使用が許されるならトポロジー的写像とは次の 2 条件を満たすものと定義できる．

・ \(x'=f(x)\) は一対一対応．
・ \(f(x)\) は連続で，逆関数 \(f^{-1}(x')\) も連続．

テキスト p.40 参照．

円とは円周のこと．中心から見た角度を考えれば，円周上の点と \(0\leqq \theta \lt 360\) が一対一に対応する．このとき計数が \(\mathfrak{c}\) になることは p.65 の注釈ですでに示した．

テキスト pp.41-43の話である．しかし，以下の議論に計数は関係しない．ここで計数に言及する理由はとくにないと思う．

記号で書けば，

「極限をとる」という手続きは，「距離」に基づいていることを注意しておく．
「だんだん近づく」というのは「距離が 0 に近づく」ということであり，\({\displaystyle \lim_{n \to \infty} {\rm P}_n={\rm P}}\) の正確な意味は， \[\qquad \lim_{n \to \infty}d\,({\rm P}_n,\,{\rm P})=0\] である．

細かいところをはっきりさせておく．点列を， \[\qquad {\rm P_1,\, P_2,\, P_1,\, P_2,\, P_1,\, P_2,\, \cdots\cdots}\] とすれば，振動発散して極限は存在しない．このような点列は除外する．つまり，全体集合 \({\rm M}\) においては極限が存在する点列のみを考える．ていねいに述べておく．

・ 点列 \({\rm P}_n\,\, (n=1,\, 2,\, 3,\, \cdots)\) は \({\rm N}\) に属する．

・ \({\rm M}\) の中では \({\displaystyle \lim_{n\to \infty} {\rm P}_n={\rm P}\in \mathrm{M}}\) が存在する．

この 2 つの条件を満たすような点列であれば，どのような点列であっても \({\rm P\in N}\) であるとき，\({\rm N}\) を閉集合という．

例をあげる．\({\rm M}\) を実数全体からなる集合（数直線），\({\rm N}=\{x \,|\, x\gt 0 \}\) とする．\({\rm N}\) は閉集合ではない．なぜなら， \[\qquad x_n=\frac{1}{n}\quad (n=1,\,2,\,3,\,\cdots)\] とすれば，\(x_n\in {\rm N}\) であり，\({\rm M}\) の中では， \[\qquad \lim_{n \to \infty}x_n=0 \in {\rm M}\] と収束する．しかし，\(0\) は \({\rm N}\) に属さないからである．

\({\rm M}\) を実数全体とすると，

・ \(0\lt x\lt 1\) とか \(2\leqq x\lt 3\) のようにいずれかの端点が含まれていない区間は閉集合ではない．

・ \(0\leqq x\leqq 1\) のように両端が含まれた区間は閉集合である．

なお，閉集合かどうかは全体集合の選び方で違ってくる（p.139 の注釈参照）．

要領を得ないところもあるが，

「トポロジー的写像で，閉集合は閉集合に対応する」

「変わらない性質」「不変な性質」という意味．

すでに書いたように（p.123の注釈），「極限」が距離に基づいているため．
簡単にこの章の流れを説明しておく．「旧世界・新世界」という語は，以後の注釈でもときどき使う．

通常の直線とか平面のような距離の存在する空間を「旧世界」とする．距離に基づいた極限もある．極限を利用して閉集合を定義する．閉集合の性質を調べる．それを性質 X とする．
次にただの集合を考える．その部分集合の一部を性質 X をもつように選んで「閉集合」と名づける．これが「新世界」である．この世界には距離も極限もない．あるのは閉集合だけ．その閉集合を使って，「遠い・近い」とか「連結（つながっていること）」という概念が表現できることを示す．

これが全体の流れである．なお，「平面上の円」や「\(0\leqq x\leqq 1\) で連続な関数」を「点」とみなした特殊な空間（pp.114-115 参照）は，距離が存在するので旧世界に属する．これらは旧世界の中の見慣れないタイプの空間として紹介されたものである．

旧世界が距離空間で，新世界が位相空間という理解でだいたいよい．ただし，あとの注釈で示すように距離空間も位相空間の一種と考えるので，ちょっと違いはある．なお，新世界には「距離も極限もない」と書いたが，「極限」についてはまったくないわけではない．しかし，本書を読む上では「ない」と思ってよい．

具体例が p.170 と p.177 に出てくる．すでに知っている世界での「A には B という性質がある」から，未知の世界で「B という性質を持つものを A と定義できないか」とする．

「閉集合」という概念があれば「位相空間」という．距離空間は「距離」が定義されている空間のことだが，距離が定義されていれば極限が定義でき閉集合が定義できる．よって，距離空間は位相空間の一種とみなす．「閉集合」という概念が「距離」に由来しているかどうかは不問とする．

\({\rm M}\) は \(0\leqq x\leqq 1\) の線分を表しており，これを全体集合としている．通常の距離で考えるので距離空間（旧世界）である．
以下を読む上では p.124 の注釈にある閉集合の定義が重要である．

（1）について．\({\rm M}\) が閉集合であるかを調べるには，「\({\rm M}\) に属する点列 \({\rm P}_n\) で，\({\displaystyle \lim_{n \to \infty}}{\rm P}_n= {\rm P \in M}\) となるもの」があれば，それがどのようなものでも \({\rm P\in M}\) であるかを調べればよい．しかし，これはあたりまえである．はじめから \({\rm P\in M}\) と仮定されているのだから，\({\rm P\in M}\) となる．全体集合は定義から自動的に閉集合になる．

（2）について．「空集合は閉集合である」とした方が都合がよいのである．

（3）について．\({\rm A+B}\) は \({\rm A}\cup {\rm B}\) のこと．\({\rm A+B}\) に属する点列 \[\qquad {\rm \textcolor{red}{P_1},\,P_2,\,\textcolor{red}{P_3},\,P_4,\,P_5,\,\textcolor{red}{P_6},\,\textcolor{red}{P_7},\,\cdots\cdots}\] で \({\displaystyle \lim_{n \to \infty}}{\rm P}_n= {\rm P \in M}\) となるものがあったとする．それぞれの点は \({\rm A}\) か \({\rm B}\) に属する（両方に属するものは適当にどちらかに割り振っておく）．少なくともどちらか一方には無限個の点があるので，それを \({\rm A}\) とする．上では赤色で示した．このとき，\({\rm A}\) に属する点のみを取り出したもの，すなわち， \[\qquad {\rm \textcolor{red}{P_1},\,\textcolor{red}{P_3},\,\textcolor{red}{P_6},\,\textcolor{red}{P_7},\,\cdots\cdots}\] のことを \[\qquad {\rm P'_1,\,P'_2,\,P'_3,\,\cdots\cdots}\] とするのである．もとの点列の極限が \({\rm P}\) なので，\({\rm P'}_n\) についても \[\qquad \lim_{n \to \infty}{\rm P'}_n= {\rm P \in M}\] である．\({\rm A}\) は閉集合なので定義より \({\rm P\in A}\) となるから，\({\rm P\in A+B}\) でもある．
結局，\({\rm A+B}\) に属する点列でその極限が \({\rm P\in M}\) であるものがあれば，それがどんなものでも \({\rm P\in A+B}\) となる．よって，定義より \({\rm A+B}\) は閉集合となる．

（4）についてはとくに難しいところはないが，\(\rm A,\, B,\, C,\,\cdots\) の集合の個数は無限個でもよいことを注意しておく．

「集合論の意味の集合 \({\rm M}\)」はテキスト p.127 と同じ．相互関係のないただのものの集まりという意味．「部分集合に閉集合が指定されたもの」は，ていねいに言うと「数ある部分集合のうちの一部が閉集合として指定されたもの」である．

この時点では閉集合がどのようにして遠近の考えにつながるのか読者にはわからない．読み進めていくとなんとなくわかってくるが，明快な説明は最後までない．理解しにくいところだと思う．

多対一については p.83 の注釈参照．全射のことである．

「一対多」ではないという意味．p.83 の注釈参照．写像として当然のことで，とくに断る必要はない．

ここから「すなわち閉集合である（p.131）」までが，ひとまとまりである．この部分は記号の使い方や説明の手順がわかりにくい．そこで，テキストとは独立した説明をする．やろうとしていることは，あとで述べる定理 7 の証明である．

まず，ここでの設定をはっきりさせておく．

ここは旧世界であり，写像（関数）が連続であるときの性質を調べたい．その性質を使って，新世界において「連続」を定義したいのである．集合 \({\rm M}\) から \({\rm M'}\) への写像を \(f(a)=a'\) という具合に書く．全射である必要はないのだが，テキストに忠実に全射とする．旧世界なので \({\rm M,\, M'}\) には距離や極限がある．通常の実数における関数 \(y=f(x)\) をイメージしてもらえばよい．写像（関数）が連続であるとは，任意の \(a\in {\rm M}\) について， \[\qquad \lim_{x \to a} f(x)=f(a)\] となることである．点列を使って言い直す．任意の \(a\in{\rm M}\) について，\({\rm M}\) に属する点列 \(a_n\) で， \[\qquad \lim_{n \to \infty} a_n=a\] となるものがあれば，それがどのような点列であっても， \[\qquad \lim_{n \to \infty}f(a_n)=f(a)\] となるとき，この写像を連続であるという．

ここで，写像が連続ならば閉集合が閉集合に写ると思うかもしれないので，それが誤りであることを示しておく．
\({\rm M,\, M'}\) を実数全体からなる集合として，\(x\) 軸，\(y\) 軸と同一視する．次のようなグラフで表される連続関数 \(y=f(x)\) を考える．

\(x\) が負の方向に進むとグラフは振幅が大きくなりながら振動する．よって，\(f(x)\) はあらゆる値をとるので全射である．\(x\) が正の方向に大きくなるときは，\(y=1\) が漸近線になる．このとき \({\rm M}\) の部分集合 \({\rm A}=\{x \,|\, x\geqq 0 \}\) は，\({\rm M'}\) の部分集合 \({\rm A'}=\{y \,|\, 0\leqq y \lt 1\}\) に写る．\({\rm A}\) は閉集合だが \({\rm A'}\) は閉集合ではない．よって，写像が連続でも閉集合が閉集合に写るとは限らない．

写像の原像について説明する．\({\rm M'}\) の部分集合 \({\rm A'}\) があるとする．このとき，\({\rm M}\) の要素 \(a\) のうち \(f(a)\) が \({\rm A'}\) に属するものの集合を \({\rm A'}\) の原像といい，\(f^{-1}({\rm A'})\) と記す．すなわち， \[\qquad f^{-1}({\rm A'})=\{a \in {\rm M} \,|\, f(a)\in {\rm A'}\}.\] 多対一の写像を考えているので \(x=f^{-1}(y)\) という逆写像があるわけではないが，記号として \(f^{-1}({\rm A'})\) と書くのである．

次の定理が成り立つ．記号はいままで通りで写像は連続とする．

定理7.　\({\rm A'}\) が閉集合ならば，\(f^{-1}({\rm A'})\) も閉集合である．

[証明] \({\rm A}=f^{-1}({\rm A'})\) とする．\({\rm A}\) に属する点列 \(a_n\,\,\,(n=1,\,2,\,\cdots)\) で，\({\displaystyle \lim_{n \to \infty} a_n=a\in {\rm M}}\) となるものをとる．\(a \in{\rm A}\) を示せば定義より \({\rm A}\) は閉集合である．
\(a_n \in f^{-1}({\rm A'})\) なので，\(f(a_n)\in {\rm A'}\) である．写像が連続なので， \[\qquad \lim_{n \to \infty}f(a_n)=f(a).\] \(f(x)\) は \({\rm M}\) から \({\rm M'}\) への写像なので，\(f(a)\in {\rm M'}\) である．よって，\(f(a_n)\,\,(n=1,\,2,\,\cdots)\) は \({\rm A'}\) に属する点列で，\({\rm M'}\) の中では \(f(a)\) に収束する．\({\rm A'}\) は閉集合なので，\(f(a) \in {\rm A'}\) となる．定義より \(a \in f^{-1}({\rm A'})={\rm A}\) となるから \({\rm A}\) は閉集合である．[証明終わり]

旧世界で連続写像に「閉集合の原像が閉集合になる」という性質があることから，新世界でこれを連続写像の定義にするということであろう．

テキスト p.41 参照．

相互関係のないただのものの集まりという意味．

「要素間の関係をことさらに無視することが集合論の主な特徴（p.27）」として，これまでにも，

「集合論の意味の集合（p.50，p.129）」
「集合論的な意味での集合（p.87）」
「集合論の意味での集合（p.103，p.127）」

「前の条件」は p.129 参照．確認の必要があるのは (3) と (4) である．理屈から考えて容易にわかる．(3) について示しておく．

「\(a\) という人を含めば，その人の子孫をすべて含む」という意味で \({\rm A,\, B}\) が閉集合とする．このとき，\({\rm A\cup B}\) が「\(a\) という人を含めば，その人の子孫をすべて含む」ことを示せばよい．\(a\in {\rm A\cup B}\) とする．\(a\) は \({\rm A}\) または \({\rm B}\) の要素である．同じことなので \({\rm A}\) の要素としよう．\({\rm A}\) が閉集合なので「\(a\) の子孫」はすべて \({\rm A}\) に含まれている．ならば，\({\rm A\cup B}\) にも「\(a\) の子孫」はすべて含まれていることになる．よって示された．

「全然異なった」は「空間的位置の遠近とは異なった」という意味．

補集合のこと．

ド・モルガンの法則による．\({\rm A}\) の補集合を \(\overline{\rm A}\) で表す．\({\rm A,\, B,\, C,\,\,\cdots}\) は開集合とする．\(\overline{{\rm A}},\,\overline{{\rm \vphantom{A}B}},\,\overline{{\rm \vphantom{A}C}},\cdots\) は閉集合である．

閉集合の条件より \({\rm \overline{A}\cup \overline{\vphantom{A}B}}\) は閉集合である．ド・モルガンの法則から， \[\qquad {\rm \overline{{A\cap B}}=\overline{A}\cup \overline{\vphantom{A}B }}\] なので，\({\rm \overline{A\cap B}}\) は閉集合．よって，\({\rm A\cap B}\) は開集合になる．

同様に，閉集合の条件より \({\rm \overline{A}\cap \overline{\vphantom{A}B}\cap \overline{C} \,\cdots}\) は閉集合である．ド・モルガンの法則から， \[\qquad {\rm \overline{A\cup B \cup C \cdots}=\overline{A}\cap \overline{\vphantom{A}B}\cap \overline{C} \,\cdots}\] なので，\(\overline{\rm A\cup B \cup C \cdots}\) は閉集合．よって，\({\rm A\cup B\cup C\,\cdots}\) は開集合になる．

なお，このページの中ほどにある図は意味が不明瞭であろう．

テキスト p.129 をまねると，条件は以下のとおり．

(1) \({\rm M}\) は「点」と称する要素の集合であり，\({\rm M}\) の部分集合にはすべて「開集合」であるかないかの指定がなされている．
(2) \({\rm M}\) 自身および空集合は開集合に指定されている．
(3) 二つの開集合の共通部分は開集合である．
(4) 有限または無限個の開集合の合併集合はまた開集合である．

そして，「開集合」の補集合を「閉集合」と定義すれば位相空間が得られるということ．

ここから「… 際立たせる働きを持っている（p.137）」までがひとまとまりである．意味のとりにくいところがあるとすれば，「補集合から分離（p.136）」，「出発点にとっても結果は同じ（p.137）」，「一つの位相空間が完全に定まってくる（p.137）」だと思う．

数直線上で，開集合を \({\rm A}=\{x \,|\, 0\lt x \lt 4 \}\)，点 \(a\) を \(x=3\) とする．補集合 \({\rm \overline{A}}\) を赤で示した．

近傍とは青で囲んだ \(2.5\lt x\lt 3.5\) のような区間のことである．ゲームか何かで赤いところが「敵陣地」とすると，\(x=3\) は，敵陣から離れた青い安全地帯の中に隔離できる．これを「分離」といっている．

「出発点にとっても結果は同じ（p.137）」，「一つの位相空間が完全に定まってくる（p.137）」については，かなり説明が省かれている．旧世界と新世界に分けて，以下のような順序で説明すればていねいである．

まず，旧世界で「近傍」を定義する．その近傍がある性質 X をもつことを示す．そして，開集合が，この近傍に関連したある性質 Y をもつことを示しておく．
次にただの集合を考える．その部分集合の一部を性質 X をもつように選んで「近傍」に指定する．この近傍を使って，部分集合のうち性質 Y をもつものを開集合と定義する．その補集合を閉集合と定義する．こうして新世界（位相空間）を作ることができる．

なお，性質 Y とは「どの点も近傍で補集合から分離できる」というはじめに述べた性質のこと．性質 X については本書で触れていない．

結局，集合を位相化する方法は 3 通りあることになる．

(1) 閉集合を指定する．その補集合を開集合とする．
(2) 開集合を指定する．その補集合を閉集合とする．
(3) 近傍を指定する．性質 Y で開集合を定義する．その補集合を閉集合とする．

本書でメインの方法は (1) であり，(2) は p.136 で簡単に説明され，(3) は pp.136-137 でさらに簡略に触れている．どの方法を使っても実質は同じであり，結果として得られる位相空間に違いはない．「出発点にとっても結果は同じ (p.137)」，「一つの位相空間が完全に定まってくる (p.137)」とは，このような意味である．

「分ける」というのは共通点のない 2 つの部分に分割するという意味．
直線は数直線として考え，\(a\) は実数とする． \[\qquad {\rm A}=\{x \,|\, x\geqq a \},\,\, {\rm B}=\{x \,|\, x\lt a \}\] とすれば分けることができる．

「連結とは分けられないもの」としたいので，これではまずい．分け方に条件を付ける必要がある．そこでアリストテレスの言葉を引用している．アリストテレスが言っているのは， \[\qquad {\rm A}=\{x \,|\, x\geqq a \},\,\, {\rm B}=\{x \,|\, x\leqq a \}\] と分割したとき，\(x=a\) が両方に含まれてしまうということ．現代的にいえば，閉集合として 2 つに分けることを考えている．

正確に述べると，「位相空間 \({\rm M}\) において，\({\rm M}\) が二つの共通点のない空でない閉集合に分けられないとき，\({\rm M}\) は連結しているという」である．なお，「空でない」とは「空集合でない」という意味．

閉集合 \({\rm A,\, B}\) あって， \[\qquad {\rm A} \neq \phi,\,\,{\rm B}\neq \phi,\,\,{\rm A\cap B}=\phi,\,\,{\rm A\cup B}={\rm M}\] となるなら \({\rm M}\) は連結ではない．このような \({\rm A, \,B}\) が存在しないなら \({\rm M}\) は連結である．

全体集合 \({\rm M}\) が連結かどうかは判定できるが，部分集合については当てはまらない．
たとえば，\({\rm M}\) を数直線とし， \[\qquad {\rm N}=\{x\,|\,1\lt x\lt 2 \,\text{ または }\,3\lt x \lt 4\}\] とする（下図の赤で示したところ）．

\({\rm N}\) は明らかに連結でないが，2 つの空でない閉集合に分けることはできない（\({\rm N}\) 自身が閉集合でないのだから当然である）．
部分集合の連結性を閉集合を使って判定することは可能なのだが，本書では触れていない．

このページに「近傍」という語が 2 回出てくる．ある点の「近傍」とは，その点を含む開集合のことと理解しておけばよい．

この部分は旧世界の話とする．数直線上に集合 \({\rm M}\) を次のようにとる． \[\qquad {\rm M}=\{-1\}\cup \{x\,|\,x\gt 0\}.\] いま，\({\rm M}\) を全体集合とする．数直線を全体集合にするのではない．
詳細は省くが，このとき，\({\rm M}\) の部分集合 \({\rm N}=\{x \,|\, x\gt 0 \}\) は定義（p.124 の注釈参照）より閉集合になる． \[\qquad x_n=\frac{1}{n}\quad (n=1,\,2,\,3,\,\cdots)\] という点列は， \[\qquad \lim_{n \to \infty}x_n=0 \notin {\rm M}\] であるから，\({\rm M}\) の中で収束しない．よって，この点列は考える必要がないことに注意してほしい．
\({\rm N}\) の補集合は，1 点からなる集合 \(\{ -1 \}\) である．閉集合の補集合なのでこれは開集合になる．

「近傍としてはその点自身をもっている」は \(\{ -1 \}\) が開集合だからである．

直前の話から，数直線上で整数からなる集合が例として思いつきやすい．しかし，すべての点が孤立点になるように位相化すると考えた方がよい．

どのような集合であれ，その部分集合をすべて閉集合に指定すれば，これは位相空間になる．補集合を考えれば，すべての部分集合が開集合でもある．あらゆる部分集合が開集合だから，1 点からなる集合 \(\{ a \}\) も開集合で，これが \(a\) だけを含む開集合になる．よって，どの点も孤立点になる．

このような位相を「離散位相」という．あらゆる部分集合が開集合かつ閉集合なので，これでは位相化の意味がない．それを「空間的関係がまったくない」と表現しているようである．

「位相が弱い（強い）」は数学の専門用語．人間社会にたとえた説明がややわかりにくく，なぜ「弱い（強い）」というのか納得がいかないかもしれない．

生物学的な子孫関係なら離婚しても系図は変わらないので，社会制度的な意味なのだろう．

これだけでは意味がわかりにくいかもしれない．種々の条件をつけることにより「ハウスドルフ空間」とか「正規空間」などいろいろなタイプの位相空間が系統的に分類されているのである．